カテゴリー: Mathematics

統計の基本となる数学に関する記事．Basic mathematics for statistics.

Derivatives

Derivatives

The derivative of y = f(x) at a point x is defined as

\displaystyle f'(x) = \lim\limits_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h} = \lim\limits_{\Delta x \rightarrow 0}\frac{\Delta y}{\Delta x} = \frac{dy}{dx}

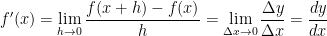
where h = Δx, Δy = f(x + h) – f(x) = f(x + Δx) – f(x) provided the limit exists.

Differentiation formulas

In the following u, v represent function of x while a, c, p represent constants. It’s assumed that the derivatives of u and v exist, i.e. u and v are differentiable.

\displaystyle \frac{d}{dx}(u \pm v) = \frac{du}{dx} \pm \frac{dv}{dx}\\\vspace{0.2 in} \frac{d}{dx}(cu) = c\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}(uv) = u\frac{dv}{dx} + v\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\left(\frac{u}{v}\right) = \frac{v(du/dx) - u(dv/dx)}{v^2}\\\vspace{0.2 in} \frac{d}{dx}u^p = pu^{p-1}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}(a^u) = a^u\ln{a}\\\vspace{0.2 in} \frac{d}{dx}e^u = e^u\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\ln{u} = \frac{1}{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\sin{u} = \cos{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\cos{u} = -\sin{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\tan{u} = \sec^2{u}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\sin^{-1}u = \frac{1}{\sqrt{1 - u^2}}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\cos^{-1}u = \frac{-1}{\sqrt{1 - u^2}}\frac{du}{dx}\\\vspace{0.2 in} \frac{d}{dx}\tan^{-1}u = \frac{1}{\sqrt{1 + u^2}}\frac{du}{dx}

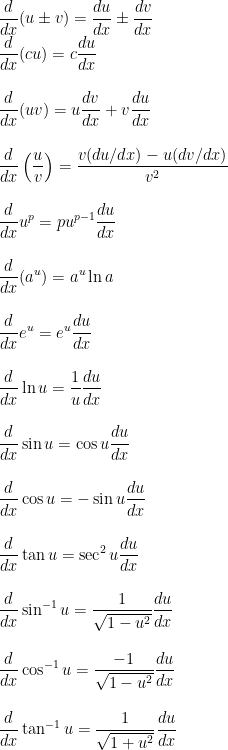
In the special case where u = x, the above formulas are simplified since in such case du/dx = 1.

Rules of algebra

If a, b, c are any real numbers, the following rules of algebra hold.

  1. Commutative law for addition
  2. Associative law for addition
  3. Commutative law for multiplication
  4. Associative law for multiplication
  5. Distributive law

Commutative law for addition

\displaystyle a + b = b + a

Associative law for addition

\displaystyle a + (b + c) = (a + b) + c

Commutative law for multiplication

\displaystyle ab = ba

Associative law for multiplication

\displaystyle a(bc) = (ab)c

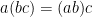
Distributive law

\displaystyle a(b + c) = ab + ac