カテゴリー: Statistics

SPSSやEXCELを用いた統計の基本的な解説．
Basic entry of statistics with SPSS and EXCEL.

Tutorial in Biostatistics Multivariable Prognostic Models: Issues in Developing Models, Evaluating Assumptions and Adequacy, and Measuring and Reducing Errors

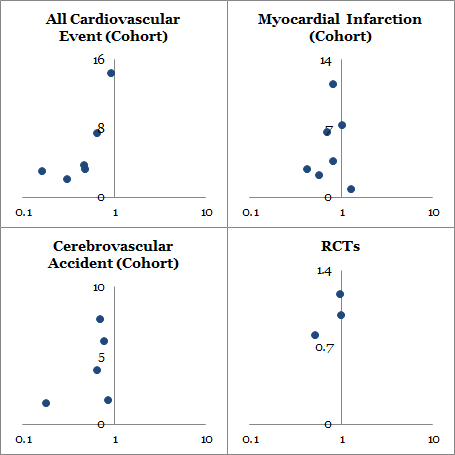
I’d like to describe of article by Harrell who has developed c index. As denoted by developer, c index is not so sensitive for detecting small difference in discriminating between two models. Such penalized maximum likelihood estimation as AIC may be more useful for detecting them.

Tutorial in Biostatistics Multivariable Prognostic Models: Issues in Developing Models, Evaluating Assumptions and Adequacy, and Measuring and Reducing Errors

Frank E. Harrell Jr, Kerry L. Lee and Daniel B. Mark

STATISTICS IN MEDICINE, VOL. 15, 361-387 (1996)

SUMMARY

Multivariable regression models are powerful tools that are used frequently in studies of clinical outcomes. These models can use a mixture of categorical and continuous variables and can handle partially observed (censored) responses. However, uncritical application of modelling techniques can result in models that poorly fit the dataset at hand, or, even more likely, inaccurately predict outcomes on new subjects. One must know how to measure qualities of a model’s fit in order to avoid poorly fitted or overfitted models. Measurement of predictive accuracy can be difficult for survival time data in the presence of censoring. We discuss an easily interpretable index of predictive discrimination as well as methods for assessing calibration of predicted survival probabilities. Both types of predictive accuracy should be unbiasedly validated using bootstrapping or cross-validation, before using predictions in a new data series. We discuss some of the hazards of poorly fitted and overfitted regression models and present one modelling strategy that avoids many of the problems discussed. The methods described are applicable to all regression models, but are particularly needed for binary, ordinal, and time-to-event outcomes. Methods are illustrated with a survival analysis in prostate cancer using Cox regression.

1. INTRODUCTION

Accurate estimation of patient prognosis is important for many reasons. First, prognostic estimates can be used to inform the patient about likely outcomes of her disease. Second, the physician can use estimates of prognosis as a guide for ordering additional tests and selecting appropriate therapies. Third, prognostic assessments are useful in the evaluation of technologies; prognostic estimates derived both with and without using the results of a given test can be compared to measure the incremental prognostic information provided by that test over what is provided by prior information.’ Fourth, a researcher may want to estimate the effect of a single factor (for example, treatment given) on prognosis in an observational study in which many uncontrolled confounding factors are also measured. Here the simultaneous effects of the uncontrolled variables must be controlled (held constant mathematically if using a regression model) so that the effect of the factor of interest can be more purely estimated. An analysis of how variables (especially continuous ones) affect the patient outcomes of interest is necessary to ascertain how to control their effects. Fifth, prognostic estimation is useful in designing randomized clinical trials. Both the decision concerning which patients to randomize and the design of the randomization process (for example, stratified randomization using prognostic factors) are aided by the availability of accurate prognostic estimates before randomization.* Lastly, accurate prognostic models can be used to test for differential therapeutic benefit or to estimate the clinical benefit for an individual patient in a clinical trial, taking into account the fact that low-risk patients must have less absolute benefit (lower change in survival probability.

To accomplish these objectives, analysts must create prognostic models that accurately reflect the patterns existing in the underlying data and that are valid when applied to comparable data in other settings or institutions. Models may be inaccurate due to violation of assumptions, omission of important predictors, high frequency of missing data and/or improper imputation methods, and especially with small datasets, overfitting. The purpose of this paper is to review methods for examining lack of fit and detection of overfitting of models and to suggest guidelines for maximizing model accuracy. Section 2 covers initial steps such as imputation of missing data, pre-specification of interactions, and choosing the outcome model. Section 3 has an overview of the need for data reduction. In Section 4, we discuss the process of checking whether a hypothesized model fits the data. In Section 5, measures of predictive accuracy are covered. These are not directly related to lack of fit but rather to the ability of the model to discriminate and be
well calibrated when applied prospectively. Section 6 covers model validation and demonstrates advantages of resampling techniques. Section 7 provides one modelling strategy that takes into account ideas from earlier sections and lists some miscellaneous concerns. Most of the methods presented here can be used with any regression model. Section 8 briefly describes some statistical software useful in carrying out the strategy summarized in Section 7. Section 9 has a detailed case study using a Cox regression model for time until death in a clinical trial studying prostate cancer.

2. PRELIMINARY STEPS

  1. Interactions between treatment and the severity of disease being treated. Patients with little disease have little opportunity to receive benefit.
  2. Interactions involving age and risk factors. Old subjects are generally less affected by risk factors. They have been robust enough to survive to their current age with risk factors present.
  3. Interactions involving age and type of disease. Some diseases are incurable and have the same prognosis regardless of age. Others are treatable or have less effect on younger patients.
  4. Interactions between a measurement and the state of a subject during a measurement. For example, left ventricular function measured at rest may have less predictive value and thus have a smaller slope versus outcome than function measured during stress.
  5. Interactions between calendar time and treatment. Some treatments evolve or their effectiveness improves with staff training.
  6. Interactions between quality and quantity of a symptom.

3. DATA REDUCTION

4. VERIFYING MODEL ASSUMPTIONS: CHECKING LACK OF FIT

4.1. Linearity assumption

4.2. Additivity assumption

4.3. Distributional assumption

5. QUANTIFYING PREDICTIVE ACCURACY

  1. To quantify the utility of a predictor or model to be used for prediction or for screening to identify subjects at increased risk of a disease or clinical outcome.
  2. To check a given model for overfitting (fitting noise resulting in unstable regression coefficients) or lack of fit (improper model specification, omitted predictors, or underfitting). More will be said about this later.
  3. To rank competing methods or competing models.

The measures discussed below may be applied to the assessment of a predictive model using the same sample on which the model was developed. However, this assessment is seldom of interest, as only the most serious lack of fit will make a model appear not to fit on the sample for which it was tailor-made. Of much greater value is the assessment of accuracy on a separate sample or a bias-corrected estimate of accuracy on the training sample. This assessment can detect gross lack of fit as well as overfitting, whereas the apparent accuracy from the original model development sample does not allow one to quantify overfitting. Section 6 discusses how the indexes described below may be estimated fairly using a validation technique.

5.1. General notions

In the simplest case, when the response being predicted is a continuous variable that is measured completely (as distinct from censored measurements caused by termination of follow-up before all subjects have had the outcome of interest), one commonly used measure of predictive accuracy is the expected squared error of the estimate. This quantity is defined as the expected squared difference between predicted and observed values, that is, the average squared difference between predicted and observed values if the experiment were repeated infinitely often and new estimates were made at each replication. The expected squared error can also be expressed as the square of the bias of the estimate plus the variance of the estimate. Here bias refers to the expected value of the estimate minus the quantity being estimated, such as the mean blood pressure. The expected squared error is estimated in practice by the usual mean squared error.

There are two other terms for describing the components of predictive accuracy: calibration and discrimination. Calibration refers to the extent of bias. For example, if the average predicted mortality for a group of similar patients is 0.3 and the actual proportion dying is 0.3, the predictions are well calibrated. Discrimination measures a predictor’s ability to separate patients with different responses. A weather forecaster who predicts a 015 chance of rain every day of the year may be well calibrated in a certain locality if the average number of days with rain is 55 per year, but the forecasts are uninformative. A discriminating forecaster would be one who assigns a wide distribution of predictions and whose predicted risks for days where rain actually occurred are larger than for dry days. If a predictive model has poor discrimination, no adjustment or calibration can correct the model. However, if discrimination is good, the predictor can be calibrated without sacrificing the discrimination (see Section 6 for a method for calibrating predictions without needing more data). Here, calibrating predictions means modifying them, without changing their rank order, such that the predictions are perfectly calibrated. van Houwelingen and le Cessie present extensive information on predictive accuracy and model validation.

5.2. Continuous uncensored outcomes

Discrimination is related to the expected squared error and to the correlation between predicted and observed responses. In the case of ordinary multiple linear regression, discrimination can be measured by the squared multiple correlation coefficient R^2, which is defined by

R^2 = 1 - (n - p)MSE/(n - 1)S^2_\gamma \cdots (1)

where n is the number of patients, p is the number of parameters estimated, MSE is the mean squared error of prediction (\sum^n_{i=1} (Y_i - \hat{y}_i)^2/(n - p),\ \hat{Y} = predicted Y), and S^2_{\gamma} is the sample variance of the dependent variable. When R^2 = 1, the model is perfectly able to separate all patient responses based on the predictor variables, and MSE = 0.

For a continuous uncensored response Y, calibration can be assessed by a scatter plot of \hat{Y} (predicted Y) versus Y, optionally using a non-parametric smoother to make trends more evident.

5.3. Discrete or censored outcomes

When the outcome variable is dichotomous and predictions are stated as probabilities that an event will occur, calibration and discrimination are more informative than expected squared error alone in measuring accuracy.

One way to assess calibration of probability predictions is to form subgroups of patients and check for bias by comparing predicted and observed responses (reference 29, pp. 140-145). For example, one may group by deciles of predicted probabilities and plot the mean response (proportion with the outcome) versus the mean prediction in the decile group. However, the groupings can be quite arbitrary. Another approach is to use a smoother such as the ‘super smoother’ or a ‘scatterplot smoother’ to obtain a non-parametric estimate of the relationship between \hat{Y} and Y. Such smoothers work well even when Y is binary. The resulting smoothed function is a nonparametric calibration or reliability curve. Smoothers operate on the raw data (Y, \hat{Y}) and do not require grouping \hat{Y}, but they do require one to choose a smoothing parameter or bandwidth.

As an example, consider a 7-variable binary logistic regression model to predict the probability that a certain disease is present. (snip)

5.4. Shrinkage

Shrinkage is the flattening of the plot of (predicted, observed) away from the 45° line, caused by overfitting. It is a concept related to regression to the mean. One can estimate the amount of shrinkage present (using external validation) or the amount likely to be present (using bootstrapping, cross-validation or simple heuristics). A shrinkage coefficient can be used to quantify overfitting or one can go a step further and use the coefficient to re-calibrate the model. Shrinkage can be defined as a multiplier \gamma of X\hat{\beta} (excluding intercept(s)) needed to make \gamma X\hat{\beta} perfectly calibrated for future data. The heuristic shrinkage estimator of van Houwelingen and le Cessie (see also reference 40) is

\displaystyle \hat{\gamma} = \frac{model\ \chi^2 - p}{model\ \chi^2} \cdots (2)

where p is the number of regression parameters (here excluding any intercept(s)) but including all non-linear and interaction effects) and the model \chi^2 is the total likelihood ratio \chi^2 statistic (computed using the full set of p parameters) for testing whether any predictors are associated with Y. For linear regression, van Houwelingen and le Cessie’s heuristic shrinkage estimate reduces to the ratio of the adjusted R^2 to the ordinary R^2 (derivable from reference 34, Eq. 70).

(snip)

Bootstrapping and cross-validation may also be used to estimate shrinkage factors. As mentioned above, shrinkage estimates are useful in their own right for quantifying overfitting, and they are also useful for ‘tilting’ the predictions so that the (predicted, observed) plot does follow the 45° line, by multiplying all of the regression coefficients by \hat{y}. However, for the latter use it is better to follow a more rigorous approach such as penalized maximum likelihood estimation, which allows the analyst to shrink different parts (for example, non-linear terms or interactions) of the equation more than other parts.

5.5. General discrimination index

Discrimination can be defined more uniquely than calibration. It can be quantified with a measure of correlation without requiring the formation of subgroups or requiring smoothing.

When dealing with binary dependent variables or continuous dependent variables that may be censored when some patients have not suffered the event of interest, the usual mean squared error-type measures do not apply. A c (for concordance) index is a widely applicable measure of predictive discrimination – one that applies to ordinary continuous outcomes, dichotomous diagnostic outcomes, ordinal outcomes, and censored time until event response variables. This index of predictive discrimination is related to a rank correlation between predicted and observed outcomes. It is a modification of the Kendall-Goodman-Kruskal-Somers type rank correlation index and was motivated by a modification of Kendall’s τ by Brown et al. and Schemper.

The c index is defined as the proportion of all usable patient pairs in which the predictions and outcomes are concordant. The c index measures predictive information derived from a set of predictor variables in a model. In predicting the time until death, c is calculated by considering all possible pairs of patients, at least one of whom has died. If the predicted survival time is larger for the patient who lived longer, the predictions for that pair are said to be concordant with the outcomes. If one patient died and the other is known to have survived at least to the survival time of the first, the second patient is assumed to outlive the first. When predicted survivals are identical for a patient pair, 0.5 rather than 1 is added to the count of concordant pairs in the numerator of c. In this case, one is still added to the denominator of c (such patient pairs are still considered usable). A patient pair is unusable if both patients died at the same time, or if one died and the other is still alive but has not been followed long enough to determine whether she will outlive the one who died.

Instead of using the predicted survival time to calculate c, the predicted probability of surviving until any fixed time point can be used equivalently, as long as the two estimates are one-to-one functions of each other. This holds for example if the proportional hazards assumption is satisfied.

For predicting binary outcomes such as the presence of disease, c reduces to the proportion of all pairs of patients, one with and one without the disease, in which the patient having the disease had the higher predicted probability of disease. As before, pairs of patients having the same predicted probability get 0.5 dded to the numerator. The denominator is the number of patients with disease multiplied by the number without disease. In this binary outcome case, c is essentially the Wilcoxon-Mann-Whitney statistic for comparing predictions in the two outcome groups, and it is identical to the area under a receiver operating characteristic (ROC) curve. Liu and Dyer advocate the use of rank association measures such as c in quantifying the impact of risk factors in epidemiologic studies.

The c index estimates the probability of concordance between predicted and observed responses. A value of 0.5 indicates no predictive discrimination and a value of 1.0 indicates perfect separation of patients with different outcomes. For those who prefer instead a rank correlation coefficient ranging from – 1 to + 1 with 0 indicating no correlation, Somers’ D rank correlation index is derived by calculating 2(c – 0.5) . Either c or the rank correlation index can be used to quantify the predictive discrimination of any quantitative predictive method, whether the response is continuous, ordinal, or binary.

Even though rank indexes such as c are widely applicable and easily interpretable, they are not sensitive for detecting small differences in discrimination ability between two models. This is due to the fact that a rank method considers the (prediction, outcome) pairs (0.01, 0), (0.9, 1) as no more concordant than the pairs (0.05, 0), (0.8, 1). A more sensitive likelihood-ratio \chi^2-based statistic that reduces to R^2 in the linear regression case may be substituted. Korn and Simon have a very nice discussion of various indexes of accuracy for survival models.

6. MODEL VALIDATION METHODS

  1. Develop the model using all n subjects and whatever stepwise testing is deemed necessary. Let D_{app} denote the apparent\ D from this model, i.e., the rank correlation computed on the same sample used to derive the fit.
  2. Generate a sample of size n with replacement from the original sample (for both predictors and the response).
  3. Fit the full or possibly stepwise model, using the same stopping rule as was used to derive D_{app}.
  4. Compute the apparent D for this model on the bootstrap sample with replacement. Call it D_{boot}.
  5. . ‘Freeze’ this reduced model, and evaluate its performance on the original dataset. Let D_{orig} denote the D.
  6. The optimism in the fit from the bootstrap sample is D_{boot} - D_{orig}.
  7. Repeat steps 2 to 6 100-200 times.
  8. Average the optimism estimates to arrive at 0.
  9. The bootstrap corrected performance of the original stepwise model is D_{app} - 0. This difference is a nearly unbiased estimate of the expected value of the external predictive discrimination of the process which generated D_{app}. In other words, D_{app}- 0 is an honest estimate of internal validity, penalizing for overfitting.
  1. Develop the model using all subjects.
  2. Compute cut points on predicted survival at 2 years so that there are m patients within each interval (m= 50 or 100 typically).
  3. For each interval of predicted probability, compute the mean predicted 2-year survival and the Kaplan-Meier 2-year survival estimate for the group.
  4. Save the apparent errors – the differences between mean predicted and Kaplan-Meier survival.
  5. Generate a sample with replacement from the original sample.
  6. Fit the full model.
  7. Do variable selection and fit the reduced model.
  8. Predict 2-year survival probability for each subject in the bootstrap sample.
  9. Stratify predictions into intervals using the previously chosen cut points.
  10. Compute Kaplan-Meier survival at 2 years for each interval.
  11. Compute the difference between the mean predicted survival within each interval and the Kaplan-Meier estimate for the interval.
  12. Predict 2-year survival probability for each subject in the original sample using the model developed on the sample with replacement
  13. For the same cut points used before, compute the difference in the mean predicted 2-year survival and the corresponding Kaplan-Meier estimates for each group in the original sample.
  14. Compute the differences in the differences between the bootstrap sample and the original sample.
  15. Repeat steps 5 to 14 100-200 times.
  16. Average the ‘double differences’ computed in step 14 over the 100-200 bootstrap samples. These are the estimates of over-optimism in the apparent error estimates.
  17. Add these over-optimism estimates to the apparent errors in the original sample to obtain bias-corrected estimates of predicted versus observed, that is, to obtain a bias- or overfitting-corrected calibration curve.

7. SUMMARY OF MODELLING STRATEGY

  1. Assemble accurate, pertinent data and as large a sample as possible. For survival time data, follow-up must be sufficient to capture enough events as well as the clinically meaningful phases if dealing with a chronic disease.
  2. Formulate focused clinical hypotheses that lead to specification of relevant candidate predictors, the form of expected relationships, and possible interactions.
  3. Discard observations having missing Y after characterizing whether they are missing at random. See reference 62 for a study of imputation of Y when it is not missing at random.
  4. If there are any missing Xs, analyse factors associated with missingness. If the fraction of observations that would be excluded due to missing values is very small, or one of the variables that is sometimes missing is of overriding importance, exclude observations with missing values. Otherwise impute missing Xs using individual predictive models that take into account the reasons for missing, to the extent possible.
  5. If the number of terms fitted or tested in the modelling process (counting non-linear and cross-product terms) is too large in comparison with the number of outcomes in the sample, use data reduction (ignoring Y) until the number of remaining free variables needing regression coefficients is tolerable. Assessment of likely shrinkage (overfitting) can be useful in deciding how much data reduction is adequate. Alternatively, build shrinkage into the initial model fitting.
  6. Use the entire sample in the model development as data are too precious to waste. If steps listed below are too difficult to repeat for each bootstrap or cross-validation sample, hold out test data from all model development steps which follow.
  7. Check linearity assumptions and make transformations in Xs as needed.
  8. Check additivity assumptions and add clinically motivated interaction terms.
  9. Check to see if there are overly-influential observation. Such observations may indicate overfitting, the need for truncating the range of highly skewed variables or making other pre-fitting transformations, or the presence of data errors.
  10. Check distributional assumptions and choose a different model if needed (in the case of Cox models, stratification or time-dependent covariables can be used if proportional hazards is violated).
  11. Do limited backwards step-down variable selection. Note that since stepwise techniques do not really address overfitting and they can result in a loss of information, full model fits (that is, leaving all hypothesized variables in the model regardless of P-values) are frequently more discriminating than fits after screening predictors for significance. They also provide confidence intervals with the proper coverage, unlike models that are reduced using a stepwise procedure, from which confidence intervals are falsely narrow. A compromise would be to test a pre-specified subset of predictors, deleting them if their total \chi^2 < 2 \times d.f.[/latex]. If the [latex]\chi^2[/latex] is that small, the subset would likely not improve model accuracy.
  12. This is the ‘final’ model.
  13. Validate this model for calibration and discrimination ability, preferably using bootstrapping. Steps 7 to 11 must be repeated for each bootstrap sample, at least approximately. For example, if age was transformed when building the final model, and the transformation was suggested by the data using a fit involving age and age, each bootstrap repetition should include both age variables with a possible step-down from the quadratic to the linear model based on automatic significance testing at each step.
  14. If doing stepwise variable selection, present a summary table depicting the variability of the list of ‘important factors’ selected over the bootstrap samples or cross-validations. This is an excellent tool for understanding why data-driven variable selection is inherently ambiguous.
  15. Estimate the likely shrinkage of predictions from the model, either using equation (2) or by bootstrapping an overall slope correction for the prediction. Consider shrinking the predictions to make them calibrate better, unless shrinkage was built-in. That way, a predicted 0.4 mortality is more likely to validate in a new patient series, instead of finding that the actual mortality is only 0.2 because of regression to the mean mortality of 0.1.

8. SOFTWARE

9. CASESTUDY

10. SUMMARY

Methods were described for developing clinical multivariable prognostic models and for assessing their calibration and discrimination. A detailed examination of model assumptions and an unbiased assessment of predictive accuracy will uncover problems that may make clinical prediction models misleading or invalid. The modelling strategy presented in Section 7 provides one sequence of steps for avoiding the pitfalls of multivariable modelling so that its many advantages can be realized.

REFERENCES:
How to calculate Harrell’s c-index to evaluate multivariate model with EXCEL VBA?
Frank E. Harrell Jr, et al: Evaluating the Yield of Medical Tests. JAMA. 1982; 247 (18): 2543 – 2546
Korn, E. L. and Simon, R. Measures of explained variation for survival data, Statistics in Medicine 9(5), 487–503 (1990)

Tutorial in Biostatistics Multivariable Prognostic Models: Issues in Developing Models, Evaluating Assumptions and Adequacy, and Measuring and Reducing Errors

　c index についての詳細な論文を見つけたので部分的に訳しておきます．太字で示したように，c index は二つのモデル間の微小な差異を検出するには向いていないことが考案者自身によって記述されています．AIC などの他の指標がより妥当かと思われます．

Tutorial in Biostatistics Multivariable Prognostic Models: Issues in Developing Models, Evaluating Assumptions and Adequacy, and Measuring and Reducing Errors

Frank E. Harrell Jr, Kerry L. Lee and Daniel B. Mark

STATISTICS IN MEDICINE, VOL. 15, 361-387 (1996)

要約

　多変量回帰モデルは有力なツールであり，臨床転帰の研究においてしばしば用いられる手法である．これらのモデルは名義変数と連続変数を混在して用いることができ，一部に観察される打切反応を扱うことができる．しかしながらモデリング手法の無批判な適用は適合不足なモデルをもたらす結果となり得るばかりか，新しい対象に対して不正確な転帰を予測する可能性がさらに高い．適合不足なモデルや過剰適合モデルを避けるためには，モデルの適合度を計測する手法を知らねばならない．適合度の正確性を計測することは打切例のある生存期間データにとっては困難になり得る．我々は予測生存確率の補正評価の手法と同じくらい容易に解釈可能な予測識別の指標について議論した．両者の予測正確性はブートストラップ法かクロスバリデーション法で偏りなく検証されるべきであり，新しいデータセットにおいて予測する前に行われるべきである．我々はいくつかのハザードの適合不足や過剰適合の回帰モデルについて議論し，議論されてきた多くの問題を避ける 1 つのモデリング戦略を提供する．ここで述べる手法は全ての回帰モデルに適用可能であり，一部の 2 値の順序尺度かつ時間イベント転帰にも必要である．Cox 回帰を用いた前立腺癌における生存分析の手法を示す．

1. 導入

　患者予後の正確な推定は多くの理由から必要である．第一に，予後の推定は，疾病について可能性のある転帰について患者自身に知らせられることである．第二に医師はその予後推定を用いて追加の検査を指示し適切な治療を選択できることである．第三に予後の評価は技術の評価に有用である．すなわち，与えられたテストの結果があってもなくても，由来する予後推定値は増加する予後の情報の計測，事前情報により提供されるテストによるが，と比較することが可能である．第四に研究者というものは一つの因子，例えば治療介入など，の多くの調整できない交絡因子が観察される観察研究における予後に対する効果を推定したがるものである．ここで，例えば回帰モデルを用いる際には数学的に定数に保持するなどして，制御されていない変数の同時効果を調整しなくてはならず，それにより関心のある因子の効果はより純粋に推定されるようになる．関心のある患者予後に，変数，特に連続変数がどう影響するかの解析は，それらがどう影響するのか確かめる必要がある．第五に，予後を推定することは無作為化比較試験をデザインするのに有用である．どの患者を無作為化するかの決定及び無作為化の仮定，例えば予後因子を用いる層別化無作為化など，のデザインの両者は無作為化前の正確な予後推定値の可用性により支援される．最後に，正確な予後モデルは，臨床研究における個々の患者にとって，低リスクの患者は絶対的に少ない利益を得なければならない（生存率にとって変化が少ない）という事実を考慮して，異なる治療法による利益の研究や臨床的な利益の推定に用いることができる．

　これらの目的を成し遂げるには，解析は予後モデルを創造しなくてはならない．元になるデータに存在するパターンを正確に反映し，他の設定や他の施設で比較可能なデータに適用した際に役立つようなモデルを．多くのモデルは以下の理由で不正確かもしれない．つまり仮定の違反，重要な予測の欠如，高頻度のデータ損失およびまたは不適切な補完方法，そして特にデータセットが小さすぎること，過剰適合など．この論文ではモデルの適合不足や過剰適合を検査する手法をレビューし，モデルの正確性を最大化するガイドラインを提案することを目的とする．2 章では初期のステップ，つまり損失データの補完，相互作用の予備仕様，および転帰モデルの選択についてをカバーする．3 章ではデータ縮減の必要性について概要を述べる．4 章では仮説モデルがデータに適合するかを検証する過程について議論する．5 章では予測精度の計測をカバーする．これらは直接には適合の欠如には関連しないが，むしろモデルを識別する能力や，前向きに適用された時によく較正されていることに関連する．6 章ではモデルの検証と再サンプリング法の利点を提示することをカバーする．7 章では前章で述べた考えやその他の懸念事項を考慮に入れた一つのモデリング戦略を提供する．ここで提示する大部分の手法はいかなる回帰モデルにも用いることができる．8 章では手短にいくつかの統計ソフトが 7 章で要約した戦略を実行するのに有用であることについて述べる．9 章では詳細なケーススタディを提示する．Cox 回帰モデルを用いて死亡に至る時間を調査した前立腺癌の臨床研究である．

2. 予備段階

  1. 治療と治療している疾患の重症度との相互作用．軽症の疾病の患者は利益を受ける機会に乏しい．
  2. 年齢やリスク因子が関与する相互作用．高齢の被験者はリスク因子に影響されにくい．
  3. 年齢と疾患の型の関与する相互作用．ある疾病は不治であり年齢は無関係に予後は同じである．
  4. 測定中の被験者の状態と測定値との相互作用．例えば，運動負荷中に比較して，安静時の左室機能は指標としての価値は少なく，より小さな傾斜を持つにすぎないだろう．
  5. 暦時間と治療法との相互作用．いくつかの治療法は進化したり，職員の訓練によりその効果が改善したりする．
  6. 症状の質と量との相互作用．

3. データの縮約

4. 検証モデルの仮定：適合不足の確認

4.1. 線形性の仮定

4.2. 加法性の仮定

4.3. 分布の仮定

5. 予測精度の定量

　予測精度の測定には少なくとも三つの用途がある．

  1. 疾病のリスクや臨床転帰のある被験者を同定するための予測やスクリーニングに用いる指標やモデルの有用性の定量．
  2. 与えられたモデルの過剰適合や適合不足の確認．過剰適合とはノイズに適合した結果，回帰係数が不安定化すること．適合不足とは不適切なモデル指定や予測因子の欠如，アンダーフィッティングのこと．これについては更に後述する．
  3. 競合する方法や競合モデルをランク付けする．

　下記で議論する測定法はモデル開発に用いたのと同じサンプルを用いた予測モデルの評価に適用できるかもしれない．しかしながら，この評価法は滅多に対象とはならない．というのは，最も深刻な適合不足モデルしかテーラーメードのサンプルに適合しないように見えるからである．非常に大きな値は分離サンプルの精度の評価または学習データの精度のバイアスを補正した推定値である．この評価は過剰適合同様に適合不足の総量を検出する一方で，元のモデルの開発するサンプルからの見かけの精度は過剰適合を定量化することには従わない．6 章においては，以下に述べる指標がいかにして検証技術を用いて相当に推定されたかを議論する．

5.1. 一般概念

　最もシンプルな事例においては，予測された反応が連続変数であり完全に測定されている時，つまりすべての被験者が関心のある転帰を取る前に経過観察を終了する打切とは異なる時，一般に用いられる予測精度は推定量の 期待二乗誤差 である．この量は，十分な回数の試行が繰り返され，その都度新しい期待値が生成されるなら，期待値と観測値との誤差の自乗の期待値，つまり予測値と観測値との平均平方差として定義される．この期待二乗誤差はまた推定量の 偏り と推定量の 分散 の和としても表現される．ここで偏りは推定量と推定された量の差の期待値のことである．例えば平均血圧などのように．期待二乗誤差は通常の平均平方誤差による実践で推定される．

　予測精度の要素を記述するにあたり，他に二つの項目がある．較正 と 判別 である．較正は偏りの程度を指す．例えば，同様の患者群の死亡率の平均が 0.3 であり，実際の死亡率が 0.3 の場合はその予測はよく較正されているという．判別とは患者を異なる反応に分離する識別能力のことである．ある気象予報士がある年の毎日の雨の確率を 0.15 と予報したら，特定の地域において年間の平均降雨日数が 55 日ならよく較正されているかも知れないが，その予報士は役に立たない．判別できる予報士とは予報の分布を広く割り付けられ，その実際に雨の降るという予報リスクが晴れの日よりも大きいものである．仮に判別の貧弱な予測モデルなら，調整や較正はモデルを全く補正できない．しかしながら，判別が良ければその予測因子は識別能力を犠牲にすることなく較正可能である．追加データなしでの予測の較正の方法については 6 章を参照のこと．ここで，予測の較正とは，それらを修飾し，それらの順位を変更することなく，その予測が完全に較正されることを意味する．van Houwelingen および Cessie は予測精度とモデル検証の追加情報を示している．

5.2. 連続非打切例の転帰

　判別は期待自乗誤差に関連し，予測値と観測された反応との相関に関連する．通常の重回帰分析においては，判別は重回帰係数 R^2 により計測される．その定義は以下である．

R^2 = 1 - (n - p)MSE/(n - 1)S^2_\gamma \cdots (1)

ここで n は患者数，p は推定パラメータ数，MSE は予測の平均自乗誤差 \sum^n_{i = 1}(Y_i - \hat{Y}_i)^2/(n - p),\ \hat{Y} = prediced\ Y, S^2_{\gamma} は従属変数の標本分散である．R^2 = 1 の時，そのモデルは予測変数に基づいて患者を完全に分離することができ，MSE = 0 となる．

　連続で打切のない反応 Y にとって，較正は \hat{Y} （予測 Y 値）と Y の散布図により評価でき，必要に応じて傾向をより明確にするためノンパラメトリック法を滑らかに用いることもできる．

5.3. 離散的または打切の転帰

　転帰変数が二値であり，予測変数があるイベントの起きる確率として記述されている場合，較正と判別は期待自乗誤差よりも多くの情報を有する．

　確率の予測の較正を評価する方法の一つは患者のサブグループを作り，予測値と観測値の偏りを調べることである．参考文献 29 の 140-145 ページを参照のこと．例えば，予測確率により十等分し，十等分した各群での平均予測に対する平均反応（転帰による割合）をプロットすれば良い．しかしながら，その群別はかなり任意である．他の方法としては ‘super smoother’ や ‘scatterplot smoother’ などの平滑化を用いることで \hat{Y} と Y との間の相関のノンパラメトリック推定を得ることである．このような平滑化は Y が二値の時でもよく働く．その結果の平滑化機能はノンパラメトリックな較正または信頼できる曲線である．平滑化は生データ (\hat{Y},\ Y) を処理し \hat{Y} の群別を要しない．しかし一つの平滑化パラメータを選択するための群別または帯域幅を要する．

　一つの例として 7 変数の二値ロジスティック回帰モデルを考えてみよう．（以下略）

5.4. 縮小推定

　縮小推定 とは過剰適合に起因する 45 ° 線から離れた（予測値，観測値）の散布図を平坦化することである．それは平均値への回帰に関連する概念である．（外部検証により）縮小する存在の量や，（ブートストラップ法やクロスバリデーション法，シンプルなヒューリスティック法により）存在しそうな量を推定することができる．縮小係数は過剰適合の定量や，モデルを再較正する係数を用いて更に一歩先を行くために用いられる．縮小推定は次のように定義される．すなわち， X\hat{\beta} （切片を除く）の乗数 \gamma であり \gamma X\hat{\beta} を将来のデータに備えて完全に較正するためのものである．van Houwelingen および Cessie によるヒューリスティック縮小推定量は以下の式である．参考文献 40 を参照のこと．

\displaystyle \hat{\gamma} = \frac{model\ \chi^2 - p}{model\ \chi^2} \cdots (2)

ここで p は回帰パラメーター数（この場合いかなる切片も除かれているが全ての非線形および相互作用を含める）とであり，モデル \chi^2 は（p 個のパラメータ全セットを用いて計算した）総尤度比 \chi^2 統計値であり，いかなる予測因子が Y に関連するかをテストする．線形回帰にとって，van Houwelingen および Cessie のヒューリスティック縮小推定量は，調整済み R^2 の通常の R^2 に対する比を削減する．参考文献 34 を参照のこと．

（中略）

　ブートストラップ法とクロスバリデーション法もまた縮小因子の推定に用いられる．上記のように，縮小推定量は過剰適合の正しい定量にとって有用であり， \hat{y} による全ての回帰係数を乗算することで，予測を『傾けて』（予測値，観測値）の点を 45 ° 線に載せるのに有用である．しかしながら，後者の用法にとっては，罰則付き最尤推定などのような，より厳格な適用に従ったほうが良い．それにより解析者は方程式の他の部分より異なる部分（例えば非線形項や相互作用項）を縮小できる．

5.5. 一般的な識別指標

　判別は較正よりもっとユニークに定義できる．サブグループ形成を要求したりや平滑化を要求したりすることなしに相関を計測することで定量できる．

　2 値の従属変数や連続変数，時に関心のあるイベントを経験せず患者の打切が発生することもあるのだが，を取り扱う際には，通常の平均値を二乗した誤差型の測定は適用されない．c index (concordance index) が広く適用される予測判定を計測する方法である．通常の連続変数，二分法の診断転帰，通常の転帰，そしてイベント反応変数までの打切時間に適用可能である．この予測判定指標は予測と実際に観測された転帰の間の順位相関に関連する．これは Kendall-Goodman-Kruskal-Somers 型の順位相関インデックスの変法であり，Kendall の τ が Brown らおよび Schemper により修正されて動機づけられたものである．

　c index は全ての患者ペアのうち，予測と転帰の一致した割合として定義される．c index はモデル中の予測変数のセットから由来する予測情報を測定する．少なくとも一人が死亡するまでの死亡に至るまでの時間を予測し，あらゆる患者ペアを考慮して c は計算される．生存期間がより長いと予測された患者が実際にも長く生存した場合，そのペアにとって予測は転帰と一致したと言える．一人の患者が死亡して，もう一人が少なくとも最初の一人の生存期間まで生存した場合は，二人目は一人目より長生きしたと前提を置くことにする．患者ペアの予測生存期間が同じ場合は 1 ではなく 0.5 を c の分子である一致ペア数に加える．この場合，c の分母に 1 を加える．そのような患者ペアも使用可能とみなす．次のような患者ペアは使用できない．つまり両名の患者とも同時に死亡した場合，また片方が死亡しもう一方が生存しているが，生存している方が死亡した方より長生きするか定義するのに十分な時間が経っていない場合である．

　c を計算するのに予測生存期間を用いる代わりに，ある固定時間に至るまでの予測生存確率を同等に用いることができる．十分に長い期待値は互いに一対一に機能する．これは例えば比例ハザード仮定が満たされていても保持される．

　疾病の有無のような 2 値の予測転帰については c は患者の全ペアの割合，疾病の予測確率が高い患者における疾病の有無の割合を低下させる．従来通り，同じ予測確率を持つ患者ペアの場合，分子に 0.5 を加える．分母は疾病のない数をかけた疾病のある患者数である．この 2 値の転帰の場合，c は基本的に二つの転帰群において予測値を比較する Wilcoxon-Mann-Whitney 統計値であり，受信者特性曲線の曲線下面積に等しい．Liu と Dyer は c indx のような順位相関測定を疫学研究でのリスク因子の影響力の定量に用いるのを支持している．

　c index は予測と観測された反応との間の一致率を推定する．値が 0.5 は全く予測精度がないことを示しており，値が 1.0 は患者予後が完全に分離していることを示している．範囲が -1 から 1 までで値が 0 の際には無相関の順位相関係数の代わりに好む人のためには，Somers’ D index が提供されており，計算式は 2(c - 0.5) である．c index であれその順位相関指標であれ，いかなる定量的予測方法をも，つまり反応が連続，順位，または 2 値であっても，定量化するために用いることができる．

　c index のような順位指標は広く適用可能で容易に解釈できるものの，二つのモデル間の微小な差異を識別する能力においてはそれほど感度は良くない．と言うのは以下の（予測，転帰）のペアの例を考えてみれば分かる．すなわち (0.01, 0) と (0.9, 1) のペアは (0.05, 0) と (0.8, 1) のペアよりも一致率が高い訳ではない．もっと感度の高い尤度比として \chi^2 に基づく統計値は線形回帰事例における R^2 に縮約され，置換されるかもしれない．Korn と Simon は生存モデルの様々な指標の精度について非常に良い議論を行っている．

6. モデル検証方法

  1. n 名の被験者の全ておよび必要とみなされるステップワイズ法を用いてモデルを開発すること．D_{app} をこのモデルからの明白な D を記述するものとする．すなわち，同じサンプルを計算して適合度を導出する順位相関のこと．
  2. 元の標本から（予測因子と反応の両者のための）標本サイズ n を生成する．
  3. D_{app} を導出したのと同じ停止規則を用いてフルモデルまたは可能性のあるステップワイズモデルに適合させること．
  4. このモデルの明白な D を置換するブートストラップ標本で計算すること．それを D_{boot} と呼ぶ．
  5. この縮約モデルを「フリーズ」させ，元のデータセットで性能を評価すること．D_{orig} で D を記述させる．
  6. 上記ステップ 2 からステップ 6 を 100 回から 200 回繰り返すこと．
  7. Optimism 推定値が 0 に到達するまで平均すること．
  8. 元のステップワイズモデルの性能を修正したブートストラップは D_{app} - 0 である．この差異は D_{app} を生成したプロセスの外部予測識別の 期待値 のほぼバイアスのない推定値である．
  1. すべての対象を用いてモデルを開発すること．
  2. 各区間内で m 名の患者が存在するような 2 年生存率を予測するカットポイントを計算すること．（典型的には 50 名とか 100 名とか）．
  3. 予測確率の各区間について，平均 2 年生存率およびカプランマイヤー 2 年生存推定値を群別に計算すること．
  4. 明白な誤差，つまり予測平均値とカプランマイヤー生存との間の誤差を保存すること．
  5. 元の標本から置換して標本を生成すること．
  6. フルモデルに適合させること．
  7. 変数選択を行い縮約モデルに適合させること．
  8. ブートストラップ標本において各患者ごとに 2 年生存率を予測すること．
  9. 以前選択したカットポイントを用いて区間に予測値を層別化すること．
  10. 各区間の 2 年目のカプランマイヤー生存率を計算すること．
  11. 各区間内の予測平均値と同じ区間内のカプランマイヤー推定値との差異を計算すること．
  12. 置換による標本で発展させたモデルを用いて元の標本における各患者の 2 年生存率を予測すること．
  13. 以前用いた同じカットポイントについて，元の標本での各群で 2 年生存率の予測平均値と対応するカプランマイヤー推定値との差異を計算すること．
  14. ブートストラップ標本と元の標本との差異の差異を計算すること．
  15. ステップ 5 からステップ 14 を 100 回から 200 回繰り返すこと．
  16. ステップ 14 でブートストラップ標本を 100 回から 200 回以上計算した「二重の差異」を平均すること．これらは明白な誤差推定値における over-optimism の推定値である．
  17. これらの over-optimism 推定値を元の標本の明白な誤差に加え，バイアスを補正した推定値を得ること．それにより観察による推定値に対して，予測されたバイアスを補正した推定値が得られる．つまりバイアスや過剰適合を補正した較正曲線を得られる．

7. モデリング戦略の概要

  1. 正確で適切で可能な限り多数のサンプルを組み立てること．生存期間データについては，慢性疾患を扱う場合には臨床的に意味のある段階のイベントを十分に補足するための経過観察期間が十分でなくてはならない．
  2. 該当する候補予測，予想される関係の形式および考えられる相互作用の仕様に至るフォーカスした臨床仮説を定式化すること．
  3. 無作為に欠損しているかどうか特徴づけられた後の欠損した Y を有する観察は捨てること．参考文献 62 には無作為に欠損していない時の Y の補完についての研究を示してある．
  4. Xs がいくつか欠損する場合，欠測と関連する因子を解析すること．欠損値により除外されていた観測の割合が非常に小さいなら，または時に欠損する変数が最優先の重要性を持つなら，欠損値を持つ観測を除外すること．そうでなければ，欠損の理由を考慮した個別の予測モデルを用いる欠損の Xs を転嫁すること．
  5. （非線形および外積条件を数える）モデリングの過程において，サンプルにおける転帰の数と比較して適合または検証する項目の数が多すぎる場合には，回帰係数を要する残存自由変数の数が許容できるまでデータを縮減（Y を無視）すること．可能性の高い縮小（過剰適合）を評価することは，どれだけのデータ縮約が適切かを決定する際に役立つだろう．あるいは，最初のモデル適合に縮小を構築すること．
  6. データを浪費するにはあまりにも貴重なので，モデル構築には全標本を使うこと．下記のステップがブートストラップやクロスバリデーションにとって困難であれば，下記の全てのモデル開発ステップにテストデータを差し出すこと．
  7. 線形性の仮定を確認し，必要なら変数変換を施すこと．
  8. 加法性の仮定を確認し，臨床的に意欲的な相互作用項を加えること．
  9. 過度に影響のある観測値があるか否か見て確認すること．そのような観測値は過剰適合，つまり高度に偏った変数の範囲の切り捨ての必要性か，またはデータの誤差を示唆するものである．
  10. 分布の仮定を確認し，必要なら異なるモデルを選択すること．（Cox モデルにおいて比例ハザード性に違反する場合は層別化や時間依存性変数が用いられる）
  11. ステップダウン変数選択の後方制約を行うこと．ステップワイズ法は過剰適合を真にaddressせず情報の損失に至るため，フルモデル適合が（つまりP 値に関係ないモデルでは全ての仮説変数を残す），有意性の指標のスクリーニング後の適合よりも，しばしばより特異的である．それらはまた適切な適用範囲を持つ信頼区間を提供するものであり，ステップワイズ処理を用いて縮減されたモデル，その信頼区間は狭いのは偽りであるが，そのようなモデルとは異なる．仮にそれらの全 \chi^2 < 2 \times d.f.[/latex] ならそれらを削除しながら，妥協は予め指定された指標のサブセットのテストになるだろう．仮にその [latex]\chi^2[/latex] が小さいならそのサブセットはモデルの正確性を改善しないだろう．
  12. ここで『最終モデル』となる．
  13. 較正および識別能力のためこのモデルを検証すること．ブートストラップ法を用いるのが望ましい．ステップ7からステップ11までを各々のブートストラップ標本に対して繰り返さなければならない．もし年齢が最終モデル構築の際に変換されたなら，そしてその変換が年齢と年齢とに関連する適合に用いるデータから示唆されたなら，各々のブートストラップ反復は可能性のある，各段階において2次方程式から線形モデルベースの自動有意性検定へのステップダウンを伴う年齢変数の両者を含んでいなければならない．
  14. 仮にステップワイズ変数選択を行うなら要約表を提示すること．要約表にはブートストラップ法やクロスバリデーション法で選択した『重要な因子』のリストの変動が示されている．これはデータ由来の変数選択がなぜ本質的に曖昧なのかを理解するのに優れたツールである．
  15. 予測式のための相関係数の全体の傾斜を，数式 (2) を使うかまたはブートストラップ法で，そのモデルから可能性の高い予測の縮約を推定すること．縮約が内蔵されていない限り予測式を縮約するよう考慮すること．それにより較正が改善する．そのように，予測された死亡率 0.4 は新しい患者シリーズにおいて検証されているようだ．平均死亡率の回帰は 0.1 であるところ実際の死亡率は 0.2 に過ぎないのだが．

8. ソフトウェア

9. ケーススタディ

10. 要約

　臨床的多変量予後モデルを開発しその較正と識別を評価する手法について述べた．詳細なモデル仮定の例および偏りのない予測精度の評価は，紛らわしく無効の臨床的予測モデルを作り出すような問題を発見するだろう．7 章に示したモデリング戦略は多変量モデリングのピットフォールを避けるステップの一つを提供し，それにより多くの進歩が確認されるだろう．

参照：
多変量モデル評価法のc-indexをEXCEL VBAで計算する
Frank E. Harrell Jr, et al: Evaluating the Yield of Medical Tests. JAMA. 1982; 247 (18): 2543 – 2546
Korn, E. L. and Simon, R. Measures of explained variation for survival data, Statistics in Medicine 9(5), 487–503 (1990)

How to get partial correlation matrix to validate multicollinearity in multivariate analysis with EXCEL?

In order to validate multicollinearity in multivariate analysis, you could investigate signs of partial correlation matrix. You could calculate partial correlation coefficient, rij rest, when you would be given covariates without xi and xj and it’s assumed that R = (rij) as correlation matrix and R-1 = (rij) as inverse matrix, respectively.

\displaystyle r_{ij\cdot rest} = - \frac{r^{ij}}{\sqrt{r^{ii}r^{jj}}}

Reverse the sign of the elements divided by square of products of the diagonal elements, they are partial correlation coefficients. The set of partial correlation coefficients is partial correlation matrix.

\displaystyle R=\left( \begin{array} {cccccc} 1 \\ r_{21} & 1 \\ \vdots & \ddots & 1 \\ r_{i1} & \ldots & r_{ij} & 1 \\ \vdots & & \vdots & \ddots & 1 \\ r_{n1} & \ldots & r_{nj} & \ldots & r_{nn-1} & 1 \\ \end{array} \right) \displaystyle R^{-1}=\left( \begin{array} {cccccc} r^{11} \\ r^{21} & \ddots \\ \vdots & \ddots & r^{jj} \\ r^{i1} & \ldots & r^{ij} & r^{ii} \\ \vdots & & \vdots & \ddots & \ddots \\ r^{n1} & \ldots & r^{nj} & \ldots & r^{nn-1} & r^{nn} \\ \end{array} \right)

When the signs didn’t match between correlation matrix and partial correlation matrix, it suggests multicollinearity. When there was linear relationship between covariates, inverse matrix of correlation matrix could not be obtained.

You could get partial correlation matrix as below. It’s assumed that you have already get correlation matrix.

  1. Get inverse matrix of correlation matrix
  2. Divide each elements of inverse matrix by square of product of diagonal elements and reverse the sign
　 A B C
1 1.000 0.800 0.300
2 0.800 1.000 -0.700
3 0.300 -0.700 1.000

1. Get inverse matrix of correlation matrix

Excel has worksheet function to get inverse matrix. You need to press the Control key, Shift key and Enter key at the same time when you confirm the argument as MINVERSE function.

{=MINVERS($A$1:$C$3)}

　 A B C
5 -0.197 1.817 1.547
6 1.817 -1.637 -1.691
7 1.547 -1.691 -0.647

2. Divide each elements of inverse matrix by square of product of diagonal elements and reverse the sign

You would have to use INDEX function, ROW function and COLUMN function. Paste following formula to the corresponding cells. The number subtracted from the return of ROW function (and COLUMN function) would change depending on the situation.

=-INDEX($A$5:$C$7, ROW()-8,COLUMN())/SQRT(INDEX($A$5:$C$7, ROW()-8, ROW()-8)*INDEX($A$5:$C$7, COLUMN(),COLUMN()))

　 A B C
9 1.000 -1.483 -2.007
10 -1.483 1.000 1.642
11 -2.007 1.642 1.000

多変量解析の多重共線性を調べるために相関行列から偏相関行列をExcelで求める方法

　多変量解析において変数間の多重共線性を調べる方法の一つに偏相関行列があります．相関行列を R = (rij) とし，その逆行列を R-1 = (rij) とすると，xi と xj 以外のすべての変数を与えた時の xi と xj の偏相関係数 rij rest は下式で表現できます．

\displaystyle r_{ij\cdot rest} = - \frac{r^{ij}}{\sqrt{r^{ii}r^{jj}}}

　逆行列の対応する要素を2つの対角要素の積の平方根で割って基準化し，符号を反転します．この偏相関係数を全ての変数の対について行列の形にまとめたものを偏相関行列と言います．

\displaystyle R=\left( \begin{array} {cccccc} 1 \\ r_{21} & 1 \\ \vdots & \ddots & 1 \\ r_{i1} & \ldots & r_{ij} & 1 \\ \vdots & & \vdots & \ddots & 1 \\ r_{n1} & \ldots & r_{nj} & \ldots & r_{nn-1} & 1 \\ \end{array} \right) \displaystyle R^{-1}=\left( \begin{array} {cccccc} r^{11} \\ r^{21} & \ddots \\ \vdots & \ddots & r^{jj} \\ r^{i1} & \ldots & r^{ij} & r^{ii} \\ \vdots & & \vdots & \ddots & \ddots \\ r^{n1} & \ldots & r^{nj} & \ldots & r^{nn-1} & r^{nn} \\ \end{array} \right)

　相関行列と偏相関行列の符号が一致しない場合は多重共線性の可能性があります．また，変数間に線形の関係がある場合は相関行列の逆行列が求まらないこともあります．

　Excelで偏相関行列を求める方法は下記の通りです．既に相関行列は求まっているものとします．

  1. 相関行列の逆行列を求める
  2. 逆行列の各要素を2つの対角要素の積の平方根で割り，符号を逆転する

 

　 A B C
1 1.000 0.800 0.300
2 0.800 1.000 -0.700
3 0.300 -0.700 1.000

1. 相関行列の逆行列を求める

　逆行列を求めるワークシート関数は Excel に標準装備されています．MINVERS 関数を用いる時の注意点として，関数の引数として相関行列を指定し，確定する際に Control キーと Shift キーと Enter キーを同時に押下する必要があります．

{=MINVERS($A$1:$C$3)}

　 A B C
5 -0.197 1.817 1.547
6 1.817 -1.637 -1.691
7 1.547 -1.691 -0.647

2. 逆行列の各要素を2つの対角要素の積の平方根で割り，符号を逆転する

　求まった逆行列の各要素から2つの対角要素のアドレスを求めるには少々工夫が必要です．INDEX 関数と ROW 関数および COLUMN 関数を組み合わせます．下式を該当セルにペーストします．ROW 関数（および COLUMN 関数）から差し引いている数値は INDEX 関数の第 1 引数の 2 次元配列の行番号（と列番号）を指定するものですので，状況によって数値は変化します．各自で対応して下さい．

=-INDEX($A$5:$C$7, ROW()-8,COLUMN())/SQRT(INDEX($A$5:$C$7, ROW()-8, ROW()-8)*INDEX($A$5:$C$7, COLUMN(),COLUMN()))

　 A B C
9 1.000 -1.483 -2.007
10 -1.483 1.000 1.642
11 -2.007 1.642 1.000

How to calculate variance inflation factor (VIF) in multivariate analysis, that influences multicollinearity?

Multicollinearity, which occurs when there is strong correlation between the variables, cause serious problems in multivariate analysis. One of the indicators of multicollinearity is variance inflation factor (VIF). It’s threshold is 10. When VIF would be 10 or larger, the impact of multicollinearity could be strong, therefore the variable should be removed.

  • Regression equation changes significantly when you add or remove a small number of data
  • Regression equation changes significantly when you applied to different data set
  • Sign of the regression coefficient is opposite to the common sense of the field
  • Although the contribution rate of regression equation is high and the model fitting is good, individual regression coefficients is not significant
  • Regression equation can not be obtained

When you encountered the phenomenon above list, you should consider multicollinearity. It’s assumed that one variable is objective and other variables are explanatory variables. You could calculate multiple correlation coefficient (R-square) by linear regression analysis with such spreadsheet software as EXCEL, and calculate VIF as following formula.

\displaystyle VIF = \frac{1}{1 - R^2}

VIF measures the impact of multicollinearity among the X’s in a regression model on the precision of estimation. It expresses the degree to which multicollinearity amongst the predictors degrades the precision of an estimate. VIF is a statistic used to measure possible multicollinearity amongst the predictor or explanatory variables. VIF is computed as (1/(1-R2)) for each of the k – 1 independent variable equations. For example, given 4 independent predictor variables, the independent regression equations are formed by using each k-1 independent variable as the dependent variable:
X1 = X2 X3 X4
X2 = X1 X3 X4
X3 = X1 X2 X4
Each independent variable model will return an R2 value and VIF value. The term to exclude in the model is then based on the value of VIF. If Xj is highly correlated with the remaining predictors, its variance inflation factor will be very large. A general rule is that the VIF should not exceed 10 (Belsley, Kuh, & Welsch, 1980). When Xj is orthogonal to the remaining predictors, its variance inflation factor will be 1.

Clearly the shortcomings just mentioned in regard to the use of R as a diagnostic measure for collinearity would seem also to limit the usefulness of R-1 , and this is the case. The prevalence of this measure, however, justifies its separate treatment. Recalling that we are currently assuming the X data to be centered and scaled for unit length, we are considering R-1 = (XTX)-1. The diagonal elements of R-1, the rii, are often called the variance inflation factors, VIFi, [Chatterjee and Price (1077)], and their diagnostic value follows from the relation
\displaystyle VIF_i = \frac{1}{1-R^2_i}
where Ri2 is the multiple correlation coefficient of Xi regressed on the remaining explanatory variables. Clearly a high VIF indicates an Ri2 near unity, and hence points to collinearity. This measure is therefore of some use as an overall indication of collinearity. Its weakness, like those of R, lie in its inability to distinguish among several coexisting near dependencies and in the lack of a meaningful boundary to distinguish between values of VIF that can be considered high and those that can be considered low. [Belsley]

References:
Cecil Robinson and Randall E. Schumacker: Interaction Effects: Centering, Variance Inflation Factor, and Interpretation Issues. Multiple Linear Regression Viewpoints, 2009, Vol. 35(1)
Belsley, D. A.: Demeaning conditioning diagnostics through centering: The American Statistics 1984; 38: 73 – 82

多変量解析における変数間の多重共線性を variance inflation factor (VIF) で検証する

　多重共線性は変数間に相関がある場合や線形関係が成立している時に発生し，多変量解析において回帰式が不安定になるなどの様々な問題を引き起こします．その指標の一つとして variance inflation factor (VIF) があり，その値が 10 以上になると多重共線性の影響が強くなるため，その変数は除去して解析すべきです．

  • 少数のデータを追加・削除しただけで回帰式が大きく変化する
  • 異なるデータに適用すると回帰式が大きく変化する
  • 回帰係数の符号がその分野の常識と逆になる
  • 回帰式の寄与率が高くモデルの適合度も良好であるが，ここの回帰係数が有意にならない
  • 回帰式が求まらない

　上記の現象が起きた際には多重共線性の存在を疑います．SPSS では通常の線形回帰分析で統計量オプションから共線性の診断をチェックして VIF を求めることができますが，表計算ソフトでも求めることができます．一つの変数を目的変数とし，他の全ての変数を説明変数として回帰分析を実行し，求まった重相関係数 R2 を用いて下式で求めます．

\displaystyle VIF = \frac{1}{1 - R^2}

VIF measures the impact of multicollinearity among the X’s in a regression model on the precision of estimation. It expresses the degree to which multicollinearity amongst the predictors degrades the precision of an estimate. VIF is a statistic used to measure possible multicollinearity amongst the predictor or explanatory variables. VIF is computed as (1/(1-R2)) for each of the k – 1 independent variable equations. For example, given 4 independent predictor variables, the independent regression equations are formed by using each k-1 independent variable as the dependent variable:
X1 = X2 X3 X4
X2 = X1 X3 X4
X3 = X1 X2 X4
Each independent variable model will return an R2 value and VIF value. The term to exclude in the model is then based on the value of VIF. If Xj is highly correlated with the remaining predictors, its variance inflation factor will be very large. A general rule is that the VIF should not exceed 10 (Belsley, Kuh, & Welsch, 1980). When Xj is orthogonal to the remaining predictors, its variance inflation factor will be 1.

Clearly the shortcomings just mentioned in regard to the use of R as a diagnostic measure for collinearity would seem also to limit the usefulness of R-1 , and this is the case. The prevalence of this measure, however, justifies its separate treatment. Recalling that we are currently assuming the X data to be centered and scaled for unit length, we are considering R-1 = (XTX)-1. The diagonal elements of R-1, the rii, are often called the variance inflation factors, VIFi, [Chatterjee and Price (1077)], and their diagnostic value follows from the relation
\displaystyle VIF_i = \frac{1}{1-R^2_i}
where Ri2 is the multiple correlation coefficient of Xi regressed on the remaining explanatory variables. Clearly a high VIF indicates an Ri2 near unity, and hence points to collinearity. This measure is therefore of some use as an overall indication of collinearity. Its weakness, like those of R, lie in its inability to distinguish among several coexisting near dependencies and in the lack of a meaningful boundary to distinguish between values of VIF that can be considered high and those that can be considered low. [Belsley]

参照：
Cecil Robinson and Randall E. Schumacker: Interaction Effects: Centering, Variance Inflation Factor, and Interpretation Issues. Multiple Linear Regression Viewpoints, 2009, Vol. 35(1)
Belsley, D. A.: Demeaning conditioning diagnostics through centering: The American Statistics 1984; 38: 73 – 82

How to calculate Harrell’s c-index to evaluate multivariate model with EXCEL VBA?

You may use Akaike information criterion (AIC) to evaluate fitting of multivariate model. You could use c-index that Harrell have proposed. Although it seems to evaluate fitting of present data set, it seems not to consider about future data set, it might result in overfitting to present data set.

  1. Make pair from data set with proportional hazard analysis
  2. Calculate risk score
  3. Compare risk score and survival time between pairs
  4. Calculate c-index

1. Make pair from data set with proportional hazard analysis

It’s assumed that sample size is N, the number of pairs could be calculated following formula.

\displaystyle _{N}C_{2} = \frac{N!}{(N-2)!2!}

It’s assumed that worksheet’s structure follows the list below.

  • The 1st line is title.
  • The 1st column is survival time, the 2nd is outcome, the 3rd is a risk score of model 1, the 4th is a risk score of model 2 and the 5th is a risk score of model 3, respectively.
  • All data type is numerical.
  • In outcome, 0 is death and 1 is censored, respectively.
Option Explicit

Sub C_Statistics()
    Dim i   As Long
    Dim j   As Long
    Dim k   As Long
    Dim Rng As Range
    Dim Ar  As Variant
    k = 0
    Set Rng = ActiveSheet.UsedRange
    Set Rng = Rng.Resize(Rng.Rows.Count - 1).Offset(1)
    Ar = Rng
    For i = LBound(Ar) To UBound(Ar) - 1
        For j = i + 1 To UBound(Ar)
            k = k + 1
        Next j
    Next i
    Debug.Print "k= " & k
End Sub

2. Calculate risk score

Risk score (R) is calculated as following formula.

\displaystyle R = \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_n X_n

\displaystyle S(t, X) = S_0(t)^{\exp(R-R_0)}

A point estimated of effect size in COX proportional hazard analysis is hazard ratio (Exp(Β)) and regression coefficient of covariate is logarithm of hazard ratio (Β). It’s assumed that risk score has been calculated.

3. Compare risk score and survival time between both of pair

It’s important that “If both of pair was censored or one of pair was censored and survival time of censored is short, they were classified as unknown”. In other words,

  • Accept the pair both of it is death
  • If one of pair is death and the survival time of death is shorter than the censored, accept it.

It’s as following VBA code. It’s assumed that it doesn’t includes equal sign if both survival time of pair were equal. 

            Select Case Ar(i, 2) + Ar(j, 2)
            Case 0
                k = k + 1
            Case 1
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 2) - Ar(j, 2)) > 0 Then
                    k = k + 1
                End If
            End Select

Furthermore, you would compare risk score and survival time between both of pair and evaluate the sign of product of the differentiation of risk score and the differentiation of survival time, respectively. It means that whether the magnitude of risk score and the length of survival time are consistent or not. It’s assumed that lower risk score means longer survival time. 

Option Explicit

Sub C_Statistics()
    Dim i   As Long
    Dim j   As Long
    Dim k   As Long
    Dim n1  As Long
    Dim n2  As Long
    Dim n3  As Long
    Dim Rng As Range
    Dim Ar  As Variant
    
    k = 0
    n1 = 0
    n2 = 0
    n3 = 0
    Set Rng = ActiveSheet.UsedRange
    Set Rng = Rng.Resize(Rng.Rows.Count - 1).Offset(1)
    Ar = Rng
    For i = LBound(Ar) To UBound(Ar) - 1
        For j = i + 1 To UBound(Ar)
            Select Case Ar(i, 2) + Ar(j, 2)
            Case 0
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 3) - Ar(j, 3)) < 0 Then
                    n1 = n1 + 1
                End If
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 4) - Ar(j, 4)) < 0 Then
                    n2 = n2 + 1
                End If
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 5) - Ar(j, 5)) < 0 Then
                    n3 = n3 + 1
                End If
                k = k + 1
            Case 1
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 2) - Ar(j, 2)) > 0 Then
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 3) - Ar(j, 3)) < 0 Then
                        n1 = n1 + 1
                    End If
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 4) - Ar(j, 4)) < 0 Then
                        n2 = n2 + 1
                    End If
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 5) - Ar(j, 5)) < 0 Then
                        n3 = n3 + 1
                    End If
                    k = k + 1
                End If
            End Select
        Next j
    Next i
    Debug.Print "n1= " & n1, "n2= " & n2, "n3= " & n3, "k= " & k
    Debug.Print "C1= " & n1 / k, "C2= " & n2 / k, "C3= " & n3 / k
End Sub

The sign of 35th line is larger than 0, it's assumed that censor is 1 and death is 0, would be reversed if censor was 0 and death was 1. The signs of 24th, 27th, 30th, 36th, 39th and 42nd would be reversed if it was assumed that higher risk score means longer survival time.

4. Calculate c-index

n1/k, n2/k and n3/k are c-index of model 1, model 2 and model 3, respectively. c-index ranges between 0 and 1. If c-index is 0.5, it means that the model doesn't fit at all. If it's closer to 0 or 1, it means that the model fits better.

Draw a pair of patients and determine which patient lived longer from his baseline evaluation. Survival times can be validly compared either when both patients have died, or when one has died and the other's followup time has exceeded the survival time of the first. If both patients are still alive, which will live longer is not known, and that pair of patients is not used in the analysis. Otherwise, it can be determined whether the patient with the higher prognostic score (ie, the weighted combination of baseline and test variables used to predict survival) also had the longer survival time. The process is repeated until all possible pairs of patients have been examined. Of the pairs of patients for which the ordering of survival time s could be　inferred, the fraction of pairs such that the patient with the higher score had the longer survival time will be denoted by c.

The index c estimates the probability that, of two randomly chosen patients, the patient with the higher prognostic score will outlive the patient with the lower prognostic score. Values of c near .5 indicate that the prognostic score is no better than a coin-flip in determining which patient will live longer. Values of c near 0 or 1 indicate the baseline data virtually always determine which patient has a better prognosis. The c index measures a probability; many clinicians are more used to dealing with a correlation index that ranges from -1 to +1. A Kendall or Goodman-Kruskal type of correlation index can easily be constructed by calculating γ = 2(c - .5), where γ is the estimated probability that the prognostic score correctly orders prognosis for a pair of patients minus the probability that it incorrectly orders prognosis. When the prognostic score is unrelated to survival time, gamma is zero. When gamma = .5, the relationship between the prognostic score and survival time is halfway between a random relationship and a perfect relationship, and the corresponding c value is .75.

References:
Frank E. Harrell Jr, et al: Evaluating the Yield of Medical Tests. JAMA. 1982; 247 (18): 2543 - 2546
Morizane Toshio: Multivariate model, International Medical Information Center 2008; 29 (3): 8 - 12

多変量モデル評価法のc-indexをEXCEL VBAで計算する

　多変量モデルの適合度の評価方法には通常赤池情報量基準 (AIC) を用いますが，Harrell らの提唱する c-index という指標もあります．c 統計値とも言い，リスクスコアの小さい（又は大きい）症例の方が生存期間が長いことが実際のデータでどれくらいの確率で正しいかを示す値です．方法は後述しますが，AIC と比較すると現在のデータに対する適合度のみを評価しており，未来のデータの予測精度への考慮がないように思えます．その意味で overfitting の可能性がある評価法と言えなくもありません．

  1. 比例ハザード解析対象となった症例から，全てのペアを作る
  2. それらのリスクスコアを調べる
  3. リスクスコアの大小および生存期間の長短を比較する
  4. c-index を計算する

1. 比例ハザード解析対象となった症例から，全てのペア（2症例ずつの組み合わせ）を作る

　サンプルサイズを N とすると，全てのペア数は下式で表現されます．

\displaystyle _{N}C_{2} = \frac{N!}{(N-2)!2!}

　ワークシート上にデータがあるとして，1行が1症例とすると，全ての行から任意の2行を取り出すコードは下記のようになります．ワークシートの構造が以下のようであると仮定します．

  • 1 行目はタイトル行である．
  • A 列は生存期間， B 列は転帰，C 列はモデル 1 のリスクスコア，D 列はモデル 2 のリスクスコア，E 列はモデル 3 のリスクスコアをそれぞれ表現する．
  • 全てのデータは数値型である．
  • B 列で死亡は 0, 打切は 1 と表現する．
Option Explicit

Sub C_Statistics()
    Dim i   As Long
    Dim j   As Long
    Dim k   As Long
    Dim Rng As Range
    Dim Ar  As Variant
    k = 0
    Set Rng = ActiveSheet.UsedRange
    Set Rng = Rng.Resize(Rng.Rows.Count - 1).Offset(1)
    Ar = Rng
    For i = LBound(Ar) To UBound(Ar) - 1
        For j = i + 1 To UBound(Ar)
            k = k + 1
        Next j
    Next i
    Debug.Print "k= " & k
End Sub

2. それらのリスクスコアを調べる

　リスクスコア (R) は下式で表現されます．予後を規定するという意味で予後スコア prognostic score とも言います．β は回帰係数，X は共変量です．R0 は全症例のリスクスコアの平均値です．S0(t) はベースラインの生存率であり，全ての説明変数が基準値である場合の各時点 t での生存率です．

\displaystyle R = \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_n X_n

\displaystyle S(t, X) = S_0(t)^{\exp(R-R_0)}

　COX 比例ハザード分析では効果量の点推定値はハザード比 (Exp(Β)) として表現され，共変量の回帰係数はハザード比の対数 (LN(Exp(Β)) = Β) として表現します．それぞれの共変量にそれぞれの回帰係数をかけた積の和がリスクスコアです．ここでは既にリスクスコアの計算は終わっているものとします．

3. リスクスコアの大小および生存期間の長短を比較する

　ここで重要な点は「2 症例とも打切例，あるいは片方が打切で打切までの期間がより短い場合は不明に分類される」との記述を条件式に表現する方法です．この条件は次のように言い換えることができます．

  • 両者とも死亡のペアを受け入れる
  • 一方が死亡の場合，死亡例の生存期間が打切例の生存期間より短いなら受け入れる

　これを VBA で表現すると以下のようになります．2 行目と 4 行目の Case 式はそれぞれ上述した条件式に該当します．5 行目は上述の条件の後者を表現したものであり，生存期間の差と転帰の差との積を取り，符号が負の場合は拒否します．参照書籍の記述によると『打切例の打切までの生存期間が同じ値かあるいは短い場合にはどちらの生存が長いかは判断することができない』とのことですので，等号は外すこととします．

            Select Case Ar(i, 2) + Ar(j, 2)
            Case 0
                k = k + 1
            Case 1
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 2) - Ar(j, 2)) > 0 Then
                    k = k + 1
                End If
            End Select

　さらにリスクスコアと生存期間とを比較します．同様にリスクスコアの差と生存期間の差との積の符号を評価します．リスクスコアの大小と生存期間の長短とが一致しているか否かを，差の積の符号に置き換えている訳です．最初に『リスクスコアの小さい（又は大きい）症例の方が生存期間が長いこと』と述べましたが，説明変数の設定によって各変数の係数の正負を逆転させ，リスクスコアの大小を逆転させることも可能です．ここではリスクスコアが小さいほど生存期間が長いという前提で話を進めます．

Option Explicit

Sub C_Statistics()
    Dim i   As Long
    Dim j   As Long
    Dim k   As Long
    Dim n1  As Long
    Dim n2  As Long
    Dim n3  As Long
    Dim Rng As Range
    Dim Ar  As Variant
    
    k = 0
    n1 = 0
    n2 = 0
    n3 = 0
    Set Rng = ActiveSheet.UsedRange
    Set Rng = Rng.Resize(Rng.Rows.Count - 1).Offset(1)
    Ar = Rng
    For i = LBound(Ar) To UBound(Ar) - 1
        For j = i + 1 To UBound(Ar)
            Select Case Ar(i, 2) + Ar(j, 2)
            Case 0
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 3) - Ar(j, 3)) < 0 Then
                    n1 = n1 + 1
                End If
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 4) - Ar(j, 4)) < 0 Then
                    n2 = n2 + 1
                End If
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 5) - Ar(j, 5)) < 0 Then
                    n3 = n3 + 1
                End If
                k = k + 1
            Case 1
                If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 2) - Ar(j, 2)) > 0 Then
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 3) - Ar(j, 3)) < 0 Then
                        n1 = n1 + 1
                    End If
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 4) - Ar(j, 4)) < 0 Then
                        n2 = n2 + 1
                    End If
                    If (Ar(i, 1) - Ar(j, 1)) * (Ar(i, 5) - Ar(j, 5)) < 0 Then
                        n3 = n3 + 1
                    End If
                    k = k + 1
                End If
            End Select
        Next j
    Next i
    Debug.Print "n1= " & n1, "n2= " & n2, "n3= " & n3, "k= " & k
    Debug.Print "C1= " & n1 / k, "C2= " & n2 / k, "C3= " & n3 / k
End Sub

　35 行目の条件式の符号は打切が 1, 死亡が 0 の際のものです．打切が 0,　死亡が 1 なら符号は逆転します．同様にリスクスコアが大きいほど生存期間が長いなら 24, 27, 30, 36, 39, 42 行目の符号は逆転します．

4. c-index を計算する

　リスクスコアと生存の関係が (1) 一致しているか，(2) 一致していないか，(3) 不明かで結果を場合分けしそれぞれの個数をカウントします．(1)/((1)+(2)) の比率が c-index です．上記では n1/k, n2/k, n3/k がそれぞれのモデルの c-index となります．c-index は 0 から 1 までの値を取りますが，0.5 の場合は全く適合していないと評価します．0 または 1 に近いほど適合が良いと評価します．

Draw a pair of patients and determine which patient lived longer from his baseline evaluation. Survival times can be validly compared either when both patients have died, or when one has died and the other's followup time has exceeded the survival time of the first. If both patients are still alive, which will live longer is not known, and that pair of patients is not used in the analysis. Otherwise, it can be determined whether the patient with the higher prognostic score (ie, the weighted combination of baseline and test variables used to predict survival) also had the longer survival time. The process is repeated until all possible pairs of patients have been examined. Of the pairs of patients for which the ordering of survival time s could be　inferred, the fraction of pairs such that the patient with the higher score had the longer survival time will be denoted by c.

The index c estimates the probability that, of two randomly chosen patients, the patient with the higher prognostic score will outlive the patient with the lower prognostic score. Values of c near .5 indicate that the prognostic score is no better than a coin-flip in determining which patient will live longer. Values of c near 0 or 1 indicate the baseline data virtually always determine which patient has a better prognosis. The c index measures a probability; many clinicians are more used to dealing with a correlation index that ranges from -1 to +1. A Kendall or Goodman-Kruskal type of correlation index can easily be constructed by calculating γ = 2(c - .5), where γ is the estimated probability that the prognostic score correctly orders prognosis for a pair of patients minus the probability that it incorrectly orders prognosis. When the prognostic score is unrelated to survival time, gamma is zero. When gamma = .5, the relationship between the prognostic score and survival time is halfway between a random relationship and a perfect relationship, and the corresponding c value is .75.

参照：
Frank E. Harrell Jr, et al: Evaluating the Yield of Medical Tests. JAMA. 1982; 247 (18): 2543 - 2546
森實敏夫：多変量モデル，あいみっく，2008; 29 (3): 8 - 12（国際医学情報センター）

Bayesian information criterion

If sample size (n) was so large enough, Bayesian information criterion (BIC), an evaluation criteria of model estimated by maximum likelihood method, would be approximated with Laplace method by integrating marginal likelihood corresponding to posterior probability of model. θ is a parameter of p-dimension and f(xn|θ) is probability distribution function, respectively.

\displaystyle BIC = -2\log f(x_n|\hat\theta) + p\log n

References:
Probability density function, expected value and variance of each probability distribution
How to calculate Akaike information criterion with probability distribution function?

ベイズ型情報量基準

　ベイズ型情報量基準 (BIC) は最尤法によって推定されたモデルの評価基準であり，サンプルサイズ n が十分に大きい時にモデルの事後確率に対応する周辺尤度を積分のラプラス法で近似して得られます．θ は p 次元パラメータ，f(xn|θ) は確率分布関数です．赤池情報量基準との違いは罰則項の係数が AIC では 2 に固定してあったのに対し， BIC ではサンプルサイズ n の自然対数を乗じているところにあります．

\displaystyle BIC = -2\log f(x_n|\hat\theta) + p\log n

参照：
確率分布ごとの確率密度関数および期待値と分散
赤池情報量基準(AIC)を確率分布関数から最尤法を用いて計算する

How to calculate Akaike information criterion with probability distribution function?

Akaike information criterion (ACI) is the most useful indicator to select variables in multivariate analysis. It’s assumed that N is free parameter number, ACI is calculated as below;

\displaystyle AIC = -2(Maximum\ Log\ Likelihood)+2N

Free parameter number of model is dimension of the space that parameter value could take in expected models. AIC is an evaluation criterion when expected model is estimated with maximum likelihood method and it indicates that log likelihood bias approximates to free parameter number included in model.

How to find maximum log likelihood? Let’s define log likelihood function as following equation;

\displaystyle l(\theta) = \sum_{\alpha=1}^{n}\log f(x_{\alpha}|\theta)

\hat\theta, that is maximum likelihood estimator, maximizes l(θ) and this is called as maximum-likelihood method. l(\hat\theta) = \Sigma_{\alpha=1}^{n}\log f(x_\alpha |\hat\theta) is called as maximum log-likelihood.

If log likelihood function (l(θ)) could be differentiable, maximum likelihood estimator (\hat\theta) would be given by solving differentiated likelihood equation.

\displaystyle \frac{\partial l(\theta)}{\partial \theta} = 0

References:
Probability density function, expected value and variance of each probability distribution

赤池情報量基準(AIC)を確率分布関数から最尤法を用いて計算する

　多変量解析の際の変数選択の一つの指標として赤池情報量基準 (Akaike information criterion) があります．詳細は成書を参考にしていただきたいのですが，N を自由パラメータ数とすると下式で求まります．

\displaystyle AIC = -2(Maximum\ Log\ Likelihood)+2N

　モデルの自由パラメータ数とは，想定したモデルに含まれるパラメータの値が動く空間の次元のことです．AIC は想定したモデルを最尤法で推定した時の評価基準であり，対数尤度のバイアスが漸近的にモデルに含まれる自由パラメータ数となることを示しています．

　最大対数尤度はどう求めるのでしょうか．ここで下式のように対数尤度関数を定義します．f(x|θ) は確率分布関数であり，分布によって形が変化します．

\displaystyle l(\theta) = \sum_{\alpha=1}^{n}\log f(x_{\alpha}|\theta)

　この l(θ) を最大化する \hat\theta が最尤推定量であり，この方法を最尤法といいます．l(\hat\theta) = \Sigma_{\alpha=1}^{n}\log f(x_\alpha |\hat\theta) を最大対数尤度と呼びます．

　対数尤度関数 l(θ) が微分可能な場合，最尤推定量 \hat\theta は尤度方程式を微分した解が 0 となる θ を求めることで求まります．

\displaystyle \frac{\partial l(\theta)}{\partial \theta} = 0

参照：
確率分布ごとの確率密度関数および期待値と分散

How to check publication bias with funnel plot?

In systematic review or meta-analyses, multiple cohort studies and randomized controlled studies are integrated and conducted more precise analysis. However, it’s impossible to avoid publication bias because non-significant studies are less likely to be posted and published. If systematic reviews or meta-analyses with publication bias were conducted, incorrect treatment would be accepted. Funnel plot is one of methods to assess whether there is publication bias or not.

Scatter plot inverse of standard error on vertical axis against odds ratio or hazard ratio on horizontal axis. If there was no publication bias, funnel plot would be symmetrical. However, if there was publication bias, funnel plot would be asymmetrical.

It is required to calculate standard error in order to draw funnel plot, if point estimated of the effect size and its 95 % confidence interval are known, they are described in most of systematic reviews and meta-analysis, you can find standard error as following;

\displaystyle \mathrm{95\%CI} = Exp(LN(\mathrm{ES})\pm1.96\times\mathrm{SE})\\ \mathrm{SE}=\frac{LN(\mathrm{ES}/\mathrm{95\%LL})}{1.96}=\frac{LN(\mathrm{95\%UL}/\mathrm{ES})}{1.96}

ES: effect size, SE: standard error, 95%CI: 95 % confidence interval, 95%LL: 95 % Lower Limit, 95%UL: 95 % Upper Limit

References:
Bias in meta-analysis detected by a simple, graphical test (pdf)
A note on graphical presentation of estimated odds ratios from several clinical trials
Funnel plot (Wikipedia)

Bias in meta-analysis detected by a simple, graphical test

Matthias Egger, George Davey Smith, Martin Schneider, Christoph Minder

Abstract

Objective

Funnel plots (plots of effect estimates against sample size) may be useful to detect bias in meta-analyses that were later contradicted by large trials. We examined whether a simple test of asymmetry of funnel plots predicts discordance of results when meta-analyses are compared to large trials, and we assessed the prevalence of bias in published meta-analyses.

Design

Medline search to identify pairs consisting of a meta-analysis and a single large trial (concordance of results was assumed if effects were in the same direction and the meta-analytic estimate was within 30% of the trial); analysis of funnel plots from 37 meta-analyses identified from a hand search of four leading general medicine journals 1993-6 and 38 meta-analyses from the second 1996 issue of the Cochrane Database of Systematic Reviews.

Main outcome measure

Degree of funnel plot asymmetry as measured by the intercept from regression of standard normal deviates against precision.

Results

In the eight pairs of meta-analysis and large trial that were identified (five from cardiovascular medicine, one from diabetic medicine, one from geriatric medicine, one from perinatal medicine) there were four concordant and four discordant pairs. In all cases discordance was due to meta-analyses showing larger effects. Funnel plot asymmetry was present in three out of four discordant pairs but in none of concordant pairs. In 14 (38%) journal meta-analyses and 5 (13%) Cochrane reviews, funnel plot asymmetry indicated that there was bias.

Conclusions

A simple analysis of funnel plots provides a useful test for the likely presence of bias in meta-analyses, but as the capacity to detect bias will be limited when meta-analyses are based on a limited number of small trials the results from such analyses should be treated with considerable caution.

Key messages

  • Systematic reviews of randomised trials are the best strategy for appraising evidences; however, the findings of some meta-analyses were later contradicted by large trials
  • Funnel plots, plots of the trials’ effect estimates against sample size, are skewed and asymmetrical in the presence of publication bias and other biases
  • Funnel plot asymmetry, measured by regression analyses, predicts discordance of results when meta-analyses are compared with single large trials
  • Funnel plot asymmetry was found in 38% of meta-analyses published in leading general medicine journals and in 13% of reviews from Cochrane Database of Systematic Reviews
  • Critical examination of systematic reviews for publication and related biases should be considered a routine procedure

出版バイアスの有無をfunnel plotにより確認する

　システマティックレビューやメタアナリシスにおいて，複数のコホート試験や無作為化比較試験のデータを統合したり累積メタアナリシスを行うなどしてより精度の高い解析を行います．しかしながらそこには出版バイアスという偏りを避ける事はできません．陰性の結果の出た試験，無効の結果の出た試験などは投稿されにくく，採用されにくい傾向があるためです．仮に出版バイアスのかかった論文ばかりでシステマティックレビューやメタアナリシスが行われた場合，誤った治療法が選択される危険性が高まります．funnel plot はそのような出版バイアスを確認するための方法です．

　横軸にオッズ比や相対危険度，ハザード比などを取り，縦軸には標準誤差の逆数を取ってプロットします．標準誤差はサンプルサイズに依存するため，サンプルサイズが大きいほど標準誤差は小さくなり，従ってその逆数は大きくなります．複数の試験を funnel plot にプロットすると，理想的な状態では漏斗をひっくり返したような左右対称の形になります．しかし出版バイアスが存在する場合はいずれか片方がすっぽり抜け落ちた形になります．

　ファンネルプロットを描くには標準誤差を求める必要がありますが，効果量の点推定値およびその 95 % 信頼区間が分かっている場合，大抵のシステマティックレビューやメタアナリシスには掲載されているものですが，下記の計算で標準誤差を求めることができます．

\displaystyle \mathrm{95\%CI} = Exp(LN(\mathrm{ES})\pm1.96\times\mathrm{SE})\\ \mathrm{SE}=\frac{LN(\mathrm{ES}/\mathrm{95\%LL})}{1.96}=\frac{LN(\mathrm{95\%UL}/\mathrm{ES})}{1.96}

ES: effect size, SE: standard error, 95%CI: 95 % confidence interval, 95%LL: 95 % Lower Limit, 95%UL: 95 % Upper Limit

References:
Bias in meta-analysis detected by a simple, graphical test (pdf)
A note on graphical presentation of estimated odds ratios from several clinical trials
Funnel plot (Wikipedia)

Bias in meta-analysis detected by a simple, graphical test

Matthias Egger, George Davey Smith, Martin Schneider, Christoph Minder

要約

対象

　ファンネルプロットはサンプルサイズに対する効果の推定値をプロットしたものであり，大規模試験により後ほど矛盾を示すメタアナリシスにおけるバイアスを検出するのに有用かもしれない．我々はメタアナリシスを大規模試験と比較した際に結果の不一致をファンネルプロットの非対称性が予測するか否か試験し，出版されたメタアナリシスのバイアスの有病率を評価した．

デザイン

　メタアナリシスと単施設大規模試験のペアを同定するため Medline 検索（結果の一致は効果が同じ方向を向いており，メタアナリシスの推定値が試験の 30 % 未満であると仮定している）． 1993 年から 1996 年までの 4 つの主要な一般的な医学雑誌から手動で検索した中から抽出した 37 のメタアナリシスと，1996 年二回目に発行された Cochrane Database of Systematic Reviews から抽出した 38 のメタアナリシス．

主要転帰計測

　精度に対する標準正規偏差の回帰から切片により測定されたファンネルプロット非対称性の程度．

結果

　同定された 8 対のメタアナリシスと大規模試験において（5 対は心血管医療から抽出され 1 対は糖尿病医療から，1 対は老人医療から，1 対は周産期医療から）4 対は一致し，4 対は一致しなかった．不一致のケースは皆，より大規模な試験で証明されたメタアナリシスだった．ファンネルプロットの非対称性は不一致の 4 対のうちの 3 対に出現していたが，一致していた対には全く出現しなかった．14 雑誌 (38 %) のメタアナリシスと 5 雑誌 (13 %) のコクランレビューにおいてファンネルプロットの非対称性はバイアスが存在することを示唆していた．

考察

　ファンネルプロットという簡便な解析により，メタアナリシスにおけるバイアスが存在するらしいことの有用なテストをもたらす．しかし検出許容はメタアナリシスが小規模試験の限定された数に基づく時に限られ，その結果は注意深く取り扱うべきである．

導入

　システマティックレビューは医療介入のリスクとベネフィットにおける最も有用なエビデンスであり，臨床研究と公衆衛生における意思決定を通知するものである．そのようなレビューは可能ならいつでもメタアナリシスに基づくべきである．『解析者によって考慮されたいくつかの独立した臨床試験を結合するか統合した統計解析は，結合可能であるべきだ』と．しかしながら，いくつかのメタアナリシスの所見は後により大規模な無作為化比較試験によって矛盾が明らかになるものである．そのような不一致は技術を広く傷つけて，最初から論争の的になってきた．メタアナリシスがミスリーディングしているように見えるのは出版バイアスや多くの他のバイアスの存在を考えれば驚くことではなく，ロケーションや選択，研究の結合により導入されるのかも知れない．

　ファンネルプロットはサンプルサイズに対する試験の効果推定値をプロットしたものであり，メタアナリシスの検証を評価するのに有用かもしれない．そのファンネルプロットというのは以下の事実に基づいている．基礎治療効果の推定における精度は，要素となる研究のサンプルサイズが増えるに従い増加する．小規模試験の結果はグラフの底辺に広く分布し，試験がより大規模になるほど狭くなる．バイアスの存在しない状態では分布は左右対称の逆さまの漏斗に似た形をする筈である．逆に，もしバイアスが存在するならファンネルプロットは歪み，非対称になる筈である．

　ファンネルプロットの価値はこれまで系統的に検証されたことがなく，対称性（または非対称性）は通常，主に視覚的な検査によって非公式に定義されただけであった．当然ながら，ファンネルプロットは観察者によって異なって解釈されてきた．我々はファンネルプロットの非対称性を数値的に計測し，同じテーマを扱ったメタアナリシスと大規模試験を比較した時，その非対称性が結果の不一致を予測するかどうかを試験した．我々はファンネルプロットの非対称性の有病率，つまりバイアスの存在を評価するために同じ方法を用いた．主要な一般医学雑誌で出版されたメタアナリシスと，Cochrane 共同計画で電子的に普及しているメタアナリシスを用いた．

方法

ファンネルプロットの非対称性の計測

　我々は線形回帰法を用いてファンネルプロットの非対称を計測し，オッズ比の自然対数スケールを用いた．現在の状況では回帰直線が原点を通るという制約を課されないにも関わらず，これは Galbraith の放射状プロットの回帰分析に対応している．標準正規偏差はオッズ比をそれ自身の標準誤差で除したと定義されるが，推定精度に対して回帰し，後者は標準誤差の逆数として定義される（回帰式は次のように定義される：SND = a + b x precision）．精度が主にサンプルサイズに依存するように，小規模試験は x 軸上では 0 に近づく．小規模試験はオッズ比の統一値からの差異を提供するが，標準誤差が大きくなるために結果として標準正規偏差は 0 点に近くなる．小規模試験は両軸共に 0 点，つまり原点に近づく筈である．逆に大規模試験は正確な推定値をもたらし，もし治療が有効なら大きな標準正規偏差をもたらす．試験の集合が同質ならその点は選択バイアスによって歪まず，標準正規偏差がゼロとなる (a = 0) 原点を通る直線上に分布するはずであり，傾き b は効果のサイズと方向を示している．この状況は左右対称のファンネルプロットに対応する．

　仮に非対称が存在する場合，系統的大規模試験の結果とは異なる結果が小規模試験で出るように，回帰直線は原点を通らない筈である．切片 a は非対称性の計測を提供する．ゼロからの偏差が大きいほど非対称がより顕著となる．小規模試験がより大きく強固な効果を有するなら，対数軸の原点より下に回帰直線が来るようになるはずである．それ故，陰性の結果は小規模試験においては大規模試験よりもより顕著な利益を示唆するはずである．ある状況では（例えばいくつかの小規模試験と1つの大規模試験が存在するような場合），推定効果の分散の逆数により解析に加重することによって検出力が上昇する．我々は加重した場合としない場合の両者について検討し，解析の結果を用いてより 0 からの偏差が大きな切片を求めた．

　異質性のすべての検査とは対照的に，ファンネルプロットの非対称性テストは異質性を特異的に評価し，この状況ではより強力なテストを提供する．しかしながら，どんな異質性の解析もメタアナリシスに含まれる試験の数に依存しており，それらは一般に小規模で，試験の統計学的検出力に限界がある．それ故我々は非対称性の根拠を P < 0.1 に設定した．そして切片を 90 % 信頼区間で表現した．同じ有意水準をメタアナリシスにおける異質性の以前の解析にも用いた．

メタアナリシスとマッチングする大規模無作為試験の同定

（中略）

結果の一致・不一致

（中略）

ファンネルプロットにおける非対称性の頻度

（中略）

結果

　メタアナリシスと大規模試験を含んでいる 8 対が同定された (Table 1)．5 対は心血管医学，1 対は糖尿病医学，1 対は老人医学，1 対は周産期医学からだった．大規模試験の精度が 14.4 であるのと比較してメタアナリシスからの効果推定値は平均精度 7.9 を有していた．4 対の一致と 4 対の不一致とがあった (Fig 1)．全例において不一致はメタアナリシスの結果であり，それらは大規模試験よりも有益な効果を証明したものであった．メタアナリシスの 4 分の 3 の不一致はメタアナリシスが統計的有意 (P < 0.1) にファンネルプロットの非対称性を示していた．一致した対のファンネルプロットは全く有意な非対称を示さなかった (Fig 2, Table 2)．

Fig.1

Fig.2

　大規模試験よりも数年早く出版された 3 つのメタアナリシスのための付加的な試験が同定された．これらは更に最近のメタアナリシスから抽出された．心筋梗塞におけるマグネシウム静注試験のメタアナリシスが 5 つの付加的な試験とともに更新された時，その切片はより大きな非対称性を示した (- 1.36 (90%CI – 2.06 to – 0.66), P = 0.05)．13 の付加的試験が心不全に対する ACE 阻害薬の試験の解析に加えられた時，散布図はまだ対称性を保っていた (切片 0.07 (- 0.53 to 0.67), P = 0.85)．氏子癇前症予防のためのアスピリンの解析が更新された時には 9 つの付加的試験が追加され，ファンネルプロットは非対称性となった (切片 – 1.49 (- 2.20 to – 0.79), P = 0.003) (Fig 3)．

Fig.3

　Figure 4 に 38 の Cochrane レビューおよび 37 の雑誌のメタアナリシスの回帰切片の分布を示した．バイアスが存在しない状態ではランダムな変動により切片はゼロ点を中心に対称性に集まる筈であり，陽性値と陰性値が同数となる筈である．しかし観察された結果はそうではなかった．分布は陰性値に偏位しており，Cochrane レビューにおいては平均で – 0.24 (- 0.65 to 0.17), 雑誌のメタアナリシスにおいては – 1.00 (- 1.50 to – 0.49) であった．Cochrane レビューでは切片には 24 の陰性値と 14 の陽性値が存在し (sign test, P = 0.10)，雑誌のメタアナリシスにおいては 26 の陰性値と 11 の陽性値が存在した (sign test, P = 0.007)．Cochrane レビューの 5 編 (13%) と雑誌メタアナリシスの 14 編 (38%) に統計的に有意な非対称性の根拠を認めた．

Fig.4

考察

　無作為化比較試験から陽性の所見だけを選択して出版することは参考文献のメタアナリシスレビューにおいて考慮すべき懸念である．仮に参考文献が治療効果の利益を証明する試験が懸念される場合，そして治療効果が無いことを証明した等しく有効な試験が出版されないままであった場合，果たしてこれらの参考文献のシステマティックレビューは臨床診療や保健政策の意思決定においてどれだけ客観的な指標として役立つであろうか．このような出版バイアスのこの潜在的に深刻な結果は暫くの間認識されており，世界規模の登録の開始時には繰り返し呼ばれてきた．試験の登録と，出版された試験とされなかった試験との結果を保持するデータベースを構築すれば問題は解決するにもかかわらず，当面それが広く提起される様子はなさそうだ．

　出版バイアスとそれに関連するバイアスを持った臨床試験はそれ故メタアナリシスとシステマティックレビューの根幹となる．ここで示した所見は次のことを示唆している．簡素な図形と統計手法がこの目的には有用であると．同じ介入に対するメタアナリシスと大規模単一試験との両者一対のこの方法を試験する時には，我々はファンネルプロットにより4分の3以上の不一致の結果に非対称性を見出した．4番目はたった6つの試験に基づいているのみで，さらなる試験により更新された時には非対称性が現れてきた．

ファンネルプロット非対称性のソース

　出版バイアスはファンネルプロットの非対称性と関連してきた．にも関わらず出版された試験においては，メタアナリシスに関連した試験を同定する確率もまたそれらの結果に影響される．英語の言語バイアス，英語以外の言語で出版された雑誌に『陰性』所見が優遇して出版されるということだが，地域と包含を作り出し，そのような研究を含める可能性が低くなる．引用バイアスの結果として『陰性』となった試験は引用される頻度がより低くなり，関連する試験を検索する際により見逃されやすくなる．『陽性』試験の結果はしばしば一度ならず報告され，メタアナリシス（複数の出版バイアス）のために配置される確率を高くする．これらのバイアスは大規模試験よりも小規模試験の方に影響を与えているようである．

Selection bias

  • Publication bias
  • Location biases

True heterogeneity

  • Size of effect differs according to study size

Data iregularities

  • Poor methodological design of small studies
  • Inadequate analysis
  • Fraud

Artefactual

  • Choice of effect measure

Chance

　非対称性の他の源は手法の品質の差から生じる．より小規模な試験は一般的に大規模試験よりも方法論的に厳しさに欠けて実施され，解析される．低質の研究はまたより大きな効果を証明しがちである．ファンネルプロットに見られる対称性の程度は，効果を測定するために実施される統計量に依存するのかもしれない．イベント発生率の高いリスクにおいて，オッズ比はリスク減少や上昇を過大評価する．このことから，小規模試験が一貫して高リスク患者において実施されるとファンネルプロットの非対称性を導く結果となる．同様に，もしイベントが一定の率で発生するなら，観察期間が延長するにともなって相対危険度は単一の値に向かって移動する筈である．大規模試験においては観察期間は小規模試験のそれよりもしばしば長くなる．最終的に非対称のファンネルプロットは偶然にしか発生しなくなる．

　ファンネルプロットに示された試験は介入における内在する同じ効果を推定しないかもしれず，それぞれの結果の間のそのような異質性はファンネルプロットの非対称性に至るかもしれない．例えば，結合された転帰が次とみなされたら，介入によって影響を受ける結合された転帰の要素のため，高リスクの患者においてのみ，かなりの利益が見られるかもしれない．コレステロール低下薬は冠動脈疾患による死亡率を低下させ，高リスク患者における全死亡率に大きな効果をもたらした．その患者とは高脂血症と同定された無症候性の患者よりも冠動脈疾患と診断の確定した患者である．これが冠動脈疾患による一貫した死亡リスク低下から，高リスク患者における患者の全死因を減少させることへと敷衍されることの根拠であり，全死亡のより大きな割合が冠動脈疾患になる筈だった患者である．仮に小規模試験が高リスク患者に実施されればファンネルプロットに非対称性を生じる結果となるはずである．

　より大規模な試験が確立する前には一般に小規模試験が実施される．現在に至るまで，対照群の治療法は実験的治療の効能を低下させる方法で改善し，変化してきた．心筋梗塞に対するマグネシウム静注の効果を調べた試験で観察された結果との乖離の説明として，そのような機序が提案されてきた．この解釈は臨床試験のデータからは支持されていないのだが．結局のところ，ある介入は大規模試験においてはより徹底されずに実施されるのかもしれず，故により小規模な試験ほど最も陽性の結果が出ることを説明しているのかもしれない．我々のメタアナリシスと大規模試験との比較を考慮すると，介入の 1 つで起こりうる，つまり入院高齢者紹介のことだが．

　それゆえ全く異なる機序が箱形に要約されたファンネルプロットにおいて導かれる可能性がある．しかしこのことは重要な記録である，研究がメタアナリシスとして結合される時には，つまりこれはいつも偏った全ての推定値と関連していると．非対称性がもっと顕著になると，バイアスの量が相当なものとなる筈である．この法則の例外は非対称性が偶然だけによって起きた場合にのみ発生する．

メタアナリシスにどの程度の頻度でバイアスが存在するか

（中略）

結論

　多くの医療介入にとって大規模で決定的な試験を欠いた状態では，無作為化比較試験に基づくシステマティックレビューはエビデンスを鑑定するための最も明らかな方法である．選択バイアスと他のバイアスはこのアプローチに極めて深刻な脅威をもたらすものの，しかしながら，信用出来なくなるメタアナリシスを避けるために注意を払うべきである．ここで議論した手法はこの目的に寄与するはずであり，恐らく存在するか又は見かけ上存在しない筈のそのようなバイアスを再現可能な計測を提供する筈である．これは簡単に計算でき，要約統計量を提供する．空間上の制限からファンネルプロットの図示が許可されない時に報告可能な要約統計量である．更に方法論的調査が求められるにもかかわらず，出版物の存在と関連するバイアスのため医療研究はルーチン作業として考慮されるべきである．しかしながらメタアナリシスがもっぱら小規模試験に基づく時には，そのようなバイアスを発掘する余地は限られている．このような状況では統計的解決法はなく，そのような解析結果はそれゆえ注意深く扱うべきである．

Key messages

  • Systematic reviews of randomised trials are the best strategy for appraising evidences; however, the findings of some meta-analyses were later contradicted by large trials
  • Funnel plots, plots of the trials’ effect estimates against sample size, are skewed and asymmetrical in the presence of publication bias and other biases
  • Funnel plot asymmetry, measured by regression analyses, predicts discordance of results when meta-analyses are compared with single large trials
  • Funnel plot asymmetry was found in 38% of meta-analyses published in leading general medicine journals and in 13% of reviews from Cochrane Database of Systematic Reviews
  • Critical examination of systematic reviews for publication and related biases should be considered a routine procedure

Systematic Review and Meta-Analysis: Anti-Tumor Necrosis Factor α Therapy and Cardiovascular Events in Rheumatoid Arthritis

Biological agents like anti-TNF α may have benefit not only in reduction of inflammation but also in reduction of cardiovascular event risk on rheumatoid arthritis. This article is systematic review that selects observational cohort studies and randomized controlled trials, the former is statistically significant but the latter is not, respectively. Analysis for publication bias suggested publication bias for all cardiovascular events, so it may be too early to conclude.

Funnelplot

Systematic Review and Meta-Analysis: Anti-Tumor Necrosis Factor α Therapy and Cardiovascular Events in Rheumatoid Arthritis

CHERYL BARNABE, BILLIE-JEAN MARTIN, AND WILLIAM A. GHALI

Arthritis Care & Research vol. 63, No. 4, April 2011, pp 522-529

Abstract

Objective

Control of rheumatoid arthritis (RA) may reduce the risk of cardiovascular events. We sought to systematically assess the association between anti–tumor necrosis factor α (anti-TNFα) therapy in RA and cardiovascular event rates.

Methods

Observational cohorts and randomized controlled trials (RCTs) reporting on cardiovascular events (all events, myocardial infarction [MI], congestive heart failure, and cerebrovascular accident [CVA]) in RA patients treated with anti-TNFα therapy compared to traditional disease-modifying antirheumatic drugs were identified from a search of PubMed (1950 to November 2009), EMBase (1980 to November 2009), and conference abstracts. Relative risks (RRs) or hazard ratios and 95% confidence intervals (95% CIs) were extracted. If the incidence was reported, additional data were extracted to calculate an incidence density ratio and its variance.

Results

The systematic review and meta-analysis include 16 and 11 publications, respectively. In cohort studies, anti-TNFα therapy was associated with a reduced risk for all cardiovascular events (pooled adjusted RR 0.46; 95% CI 0.28, 0.77), MI (pooled adjusted RR 0.81; 95% CI 0.68, 0.96), and CVA (pooled adjusted RR 0.69; 95% CI 0.53, 0.89). Meta-analysis of RCTs also produced a point estimate indicating lower risk of cardiovascular events, but this was not statistically significant (pooled RR 0.85; 95% CI 0.28, 2.59).

Conclusion

Anti-TNFα therapy is associated with a reduced risk of all cardiovascular events, MI, and CVA in observational cohorts. There was heterogeneity among cohort studies and possible publication bias. The point estimate of the effect from RCTs is underpowered with wide 95% CIs, and cardiovascular events were secondary outcomes, but RCTs also demonstrated a trend toward decreased risk.

Systematic Review and Meta-Analysis: Anti-Tumor Necrosis Factor α Therapy and Cardiovascular Events in Rheumatoid Arthritis

　関節リウマチに対する生物学的製剤の使用は炎症を効率よく改善させるだけでなく，心血管イベントリスクを減少させるかもしれないという系統的レビューです．観察コホート試験と無作為化比較試験を選択したのですが無作為化比較試験では統計的有意ではなかったとのことです．コホート試験では統計的有意な結果が出ましたが出版バイアスの可能性があり，結論を出すには時期尚早と思われます．

Funnelplot

Systematic Review and Meta-Analysis: Anti-Tumor Necrosis Factor α Therapy and Cardiovascular Events in Rheumatoid Arthritis

CHERYL BARNABE, BILLIE-JEAN MARTIN, AND WILLIAM A. GHALI

Arthritis Care & Research vol. 63, No. 4, April 2011, pp 522-529

対象

　関節リウマチの制御は心血管イベントのリスクを減弱させているかもしれない．我々は抗TNF-α 治療と心血管イベント発症率との間の相関を系統的に評価しようとした．

方法

　観察コホートと無作為化比較試験のうち，抗 TNF-α 治療と伝統的な DMARDs 治療法とを比較したリウマチ患者で心血管イベント（全イベント，心筋梗塞，うっ血性心不全，脳血管疾患）について記載のあるものを PubMed および EMBase およびカンファレンスの要約から同定した．相対危険度またはハザード比とその 95% 信頼区間を抽出した．インシデントが報告された場合は罹患密度とその分散を計算するために付加情報も抽出した．

結果

　系統的レビューとメタ解析はそれぞれ 16 編と 11 編が含まれた．コホート試験においては抗 TNF-α 治療は全血管イベントの相対危険度と相関しており，調整後の相対危険度と 95% 信頼区間はそれぞれ 0.46 (0.28-0.77) であった．心筋梗塞については 0.81 (0.68- 0.96) であった．また脳血管疾患については 0.69 (0.53 -0.89) であった．無作為化比較試験のメタ解析では心血管イベントのリスクの低下を示唆する点推定値が得られたが，統計的有意ではなかった（相対危険度 0.85,95% 信頼区間 0.28-2.5）．

結論

　観察研究における抗 TNF-α 治療は全心血管イベント，心筋梗塞，脳血管障害のリスク低下と相関している．コホート試験と出版バイアスとの間には異質性がある．無作為化比較試験での点推定値は 95% 信頼区間で力不足であり，心血管イベントは secondary outcome であったが，無作為化比較試験はリスクを減少させる傾向にあることを証明した．

導入

　関節リウマチは慢性炎症性疾患であり，心血管イベント発症リスクの増加と関連している (1-3)．このことは伝統的な心血管リスク因子と不適切に治療された関節リウマチの炎症性環境 (4との両者に寄与している．過去 15 年間で関節リウマチに対する治療戦略は劇的に変化しており，DMARDs と生物学的製剤によって早期に寛解達成することが治療目標となった．関節リウマチ患者における心血管リスク因子が注目されるようになったのは，この集団における心血管死亡率と罹患率の上昇が広く認識されるようになったことによる．

　リウマチの疾患活動性を適切に維持することで炎症を有効に治療することは心血管イベントのリスクを減少させるかもしれない．最近の系統的レビューによると，メソトレキセートが心血管イベントリスクに対して有効であると明らかになった (5)．抗 TNF α 治療はメソトレキセートや他の標準的 DMARDs が失敗した患者にとって切り札となる治療法である．抗 TNF α 治療が付加的にリスクを抑止することは明らかで，心血管疾患の代理マーカーに良い意味でのインパクトを有することが証明されたように．以下の点が明らかになった，例えば循環血中の CRP や IL-6 など．他の内皮機能測定値のうち，頸動脈内膜肥厚と flow mediated dilatation を改善させる (6-7)．

　治療されたリウマチ患者の大規模コホートの組立は特異的な治療法の転機を評価する機会を国際的に与えており，同時に副作用の情報をも提供している．抗 TNF α 治療の転帰と副作用に関する有意な量のエビデンスは無作為化比較試験により蓄積される．我々はどんな可能性でも抗 TNF α 治療の心血管イベントリスクに関する臨床効果を定義するため，エビデンスのこれらの2つのソース，つまりコホート試験と無作為化比較試験とを系統的にレビューしたかった．特に，我々の疑問は次のようなものであった，リウマチ患者における抗 TNF α 治療と DMARDs 治療とを比較して心血管イベントリスクは観察コホートと無作為化比較試験とで同定されるか否かを試驗しているかである．

対象と方法

　系統的レビューとメタ解析は Preferred Reporting Themes for Systemic Revs ad Meta Analysis Group ガイドラインで概説されたフレームワークに従って実施され，報告における標準化と品質を向上させた (8)．レビューのプロトコールは文献検索の前に開発された（著者の連絡先から可能な検索）．

データソースとリサーチ

　我々は PubMed (1950 – 2009/11/1) および EMBase (1980 – 2009/11/1) の系統的文献検索を実施した．関連する記述のレビュー原著および参考文献リストの鍵となる原著はさらに関連出版物から検索した．最近出版された専門家についてはどんな出版されていないデータについても接触して同定した．2007 年から 2009 年のリウマチ及び心臓病学会 (European League Against Rheumatism, Ameican College of Rheumatology, Canadian Rheumatology Association,American College of Cardiology, American Heart Canadian Cardiovascular Society) の年次総会の会議抄録もレビューした．詳細な明細や統計解析において付加的な情報が要求されるインスタンス内で対応する筆者に直接接触した．タイトルや抄録で使われるキーワードや同義語を使用するにあたり，また医療対象者の見出しに使用するにあたり，３つのテーマが創造された．それらのテーマは『関節リウマチ』『心血管イベント』『抗 TNF α 治療』であった．これらの３つのテーマは抗 TNF α 治療を受けているリウマチ患者に発生する心血管イベント報告した研究を同定するため，ブール演算子の AND により結合して用いられた．加えて，『抗 TNF 治療』『関節 リウマチ』のテーマは結合され，我々はCochrane共同計画無作為化比較試験のフィルターを適用し，関節リウマチ患者で抗 TNF α 治療を受けている無作為化比較試験を同定した (9)．

試験の選択

　2 名の著者 (CB and B-JM) は独立して原著をスクリーニングして全文レビューした．全タイトルと要約を先述の検索方法で取得してスクリーニングした．言語に制約は設けなかった．原著にリウマチ患者が抗 TNF α 治療を受け，心血管イベントをも報告している報告があれば含めた．我々の焦点が臨床的イベントに置かれていたため，動脈硬化の代理マーカーのみを報告しているものは除外した．最初のスクリーニングにおける賛同は 99.7 % であった．どんな原著であれ最初のスクリーニングで２名のいずれかの筆者により研究質問にとって陽性の関連を有しているとして同定されたものは全文レビューした．

　次のステップとして全文レビューに着手した．この段階では２つの研究デザインを考慮した．つまり観察コホート試験と無作為化比較試験である．リウマチ患者が抗 TNF α 治療と DMARDs と比較した治療を受け，心血管イベント（心筋梗塞，うっ血性心不全，脳血管障害）について言及したオリジナルのデータを報告していれば，原著には系統的レビューも含まれた．我々は観察期間が 26 週未満の報告は除外した．いかなる同定された有効性も確実らしいということと，短い治療期間における変化でないと保証するためである．第２段階で観察された合意は 95.9 % であった．２名の筆者間での食い違いは３人目の筆者 (WG) を交えた協議によって解決した．定量的メタ解析に含まれた研究は，同等の２群間での相対危険度の定義を可能にするための十分なデータを有していなければならないとされた．

データ抽出と品質評価

　データは両著者によって独立に抽出した．我々は患者の人口動態，場所の調査，観察期間を記録した．比較治療（メソトレキセートや DMARDs），リウマチの疾患活動性因子，心血管リスク因子または既存の条件も記録した．相対危険度またはハザード比および関連する 95% 信頼区間は直接抽出した．インシデントが報告された際には，罹患密度とその分散を計算するために両群でのイベント数と患者-年のフォローアップもまた抽出した．回帰モデルにおいて調整共変量が作成された場合にはデータ抽出の際に最も調整された相対危険度と同等のものを選択した．抗 TNF α 治療群と一般的リウマチ治療群との比較においては一般治療群が特定されない状況では DMARDs 治療を受けていると仮定した．研究品質を評価するのに必要な情報は Egger らによる観察コホート試験と無作為化比較試験のためのチェックリストに従い抽出した (10)．

データ合成と統計解析

　関連性の尺度を計算するための十分なデータを公表していない研究はオリジナルの出版として公表された．彼らが同じ転帰を報告したとしても，我々は２つの研究デザインを１つにまとめなかった．というのは，メタ解析に十分な情報を持つコホート試験のために我々は，各々の転帰のための独立した解析における全心血管イベント，心筋梗塞，脳血管障害，うっ血性心不全の調整済み相対危険度を定義したからである．ハザード比と罹患密度比は直接相対危険度として考慮される．オッズ比として表現される結果は Zhang と Yu により記述された方法 (11) で相対危険度に変換された．メタ解析に十分な情報を持つ無作為化比較試験のため，抗 TNF α 治療群と対照群との間のイベントの相対危険度を計算した．我々はメタ解析には Stata (Stata-Corp) バージョン 10.0 を用い，観察研究を横断した対数変換した相対危険度を計算し，『めちゃくちゃな』無作為化比較試験のための相対危険度を指示した．観察コホートのため，我々は DerSimonian and Laird random-effect モデルを採用して全心血管イベントの転帰を評価し，fixed-effect モデルを採用して心筋梗塞と脳血管疾患の転帰を評価した．我々は fixed-effects モデルを採用して無作為化比較試験を評価した．コホート試験と無作為化比較試験の相対危険度および対数相対危険度並びにそれらの 95% 信頼区間を要約するために forest plot 法が開発された．コホート試験における経時的なエビデンス蓄積効果を同定するために， metacum なコマンドが使われた．

　研究の間の異質性は Cochrane Q 統計値および I2 統計値を用いて評価した．１つのコホート試験には Yates 変換が適用され，解析を実行した．というのはその研究 (Geborek et al, 12) にはイベントが発生しなかったためである．Begg test および funnel plot による可視化解析は出版バイアスを評価するために用いた．

結果

　全部で 5,022 の要約がデータベース検索方法から同定された．付加的な 7 つの出版物は手動での検索および協議の手続きにより同定された．5,029 の要約のうち 97 編が全文レビューに選択された (Figure 1)．予め指定しておいた適合基準に基づいて 16 研究が系統的レビューに選択された．それらの研究の特徴を Table 1 に示した．要約すると，我々は 13 のコホート試験（106,202 名の患者）と 3 つの無作為化比較試験（2,126 名の患者）を同定した．イベントは研究によってばらつきがあり，全心血管イベント（5 つのコホート試験および 1 つの無作為化比較試験），心筋梗塞（6 つのコホート試験および 2 つの無作為化比較試験），脳血管疾患（4 つのコホート試験），うっ血性心不全（6 つのコホート試験）を含んでいた．4 つのコホート試験が全ての抗 TNF α 治療法を使用したと報告し，5 つのコホート試験が infliximab および etanercept に特化して報告し，4 つのコホート試験は infliximab, etanercept および adalimumab の使用を報告した．1 つの無作為化比較試験が infliximab, etanercept, adalimumab の使用を報告した．我々の検索には golimumab も含まれていたにもかかわらず，同定された研究にこの薬剤を使用したものはなかった．Table 2 に報告されたリスク測定および観察コホートにおける解析に用いた調整方法および共変量を示した．データ抽出を実施した後にメタ解析に耐えうると同定されたのは，たった 8 編のコホート試験と 3 つの無作為化比較試験だけであった．

研究品質

　コホート試験と無作為化比較試験は Egger (10) らによって提案された要素に従って評価された．Table 1 および Table 2 に研究品質を評価するのに要求される情報をまとめて示す．コホート試験の大部分においては患者サンプリングと転帰の評価は，コホート試験デザインにおける固有の限界を，出来るだけ客観的に与えられる．2 編のコホート試験 (Listing et al, 2008 [13], Dixon et al, 2007 [14]) は高品質と考えられ，11 編は中等度の品質とされた．中等度の品質の限界の大部分は，代表とコホートの疾患コースにおける時間ポイントを定義する情報が提供されない欠如である．1 つを除いた全てのコホート試験にとって，コホートに組み入れられた後の治療法は標準化もされず無作為化もされていなかった．現実の観察研究に期待されているように．5 つのコホート試験はベースラインでのリウマチや心血管危険因子について調整しておらず，これらのうち，事前に指定したメタ解析のための適合基準に合致していたのはたった 3 編であった．全ての無作為化比較試験は高品質であり，3 編の研究は盲検化，無作為割付，試験中の患者の流れを透明化する報告といったキー要素を有していた．

コホート試験結果

　全心血管イベント，心筋梗塞，脳血管障害を発症した例についての抗 TNF α 治療効果を forest plot を Figure 2 に示す．要約すると，抗 TNF α 治療は全心血管イベント発症のリスク減少と相関し（調整相対危険度は 0.46, 95% 信頼区間は 0.28-0.77），心筋梗塞については (0.81, 95%CI 0.68-0.96)，脳血管障害は (0.69, 95%CI 0.53-0.89)であった．これらのエンドポイントの解析によって研究間の異質性が明らかになった．全心血管イベントに対する I2 = 89.3%, (異質確率 P < 0.001), 心筋梗塞については I2 = 39.9% (P = 0.139), 脳血管疾患については I2 = 39.3% (P = 0.176) であった．各々のエンドポイントに対して出版バイアスを解析した．外観検査は Begg’s test が有意な値 (P = 0.05) をもって全ての心血管イベントの出版バイアスを示唆していた．抗 TNF α 治療によって心血管イベントが増えたとする報告は少なかった．funnel plot による心筋梗塞と脳血管疾患は対照的であり，Begg’s test の値はそれぞれ P = 0.851, P = 0.174 であった．各々のエンドポイントについて報告した少数の研究では視覚的かつ統計的な funnel plot の解釈に限界があると報告していた．

　全てのコホート試験に対する累積メタ解析が実施され，転帰としての心筋梗塞を報告した研究について経時的な変化が起きるか評価し，この解析によって年余に渡り抗 TNF α 治療との間に有意な変化はないことが明らかになった．

　うっ血性心不全を転帰として報告した研究においては利用に足る数が十分でなかったことや，エンドポイントに関して一貫性を欠いた定義，協会の方向性が不確実に去るなどしたため，着手できなかった．我々はそれにもかかわらず，このエンドポイントについて報告した 6 つの研究に関する所見を提供した．Wolfe and Michaud は抗 TNF α 治療を受けた群では DMARDs 治療を受けた群と比較して全心不全イベント罹患率が 1.2 % (95%CI -1.9 – -0.5) 減少することを報告したが，発生例においては有意ではなかった (15)．Carmona らは抗 TNF α 曝露群とメソトレキセート曝露群とのうっ血性心不全症例の率比が 0.14 (95%CI 0.06-0.32) であると同定した (16)．Listing らのグループはうっ血性心不全発症したのは抗 TNF α 群では 25 名のうち 16 名であり，対してDMARDs でマッチさせた対照群では 25 名中 20 名であったと同定し，相対危険度は 0.8 (95%CI 0.56-1.14) であった (13)．一方，Gole らの研究では抗 TNF α 治療群と DMARDs 群との間に心不全発症率に本質的な差異はないと明らかになった（103 名のうち 7 名に対して 100 名に対して 8 名, 相対危険度 0.85, 95%CI 0.32-2.26）(17)．他の２つの研究では抗 TNF α 群で心不全のリスクが上昇した．Curtis らは 4.4 倍のリスク上昇を同定し，Setoguchi らは調整ハザード比が 2.1 (95%CI 1.0-4.3) と同定した (18, 19)．

無作為化比較試験結果

　3 つの無作為化比較試験のメタ解析により，心血管イベント発症率の相対危険度が抗 TNF α 群において DMARDs 群と比較して 0.85 (95%CI 0.28-2.59) であると明らかになった (Figure 3)．この 95% 信頼区間はとても広く，コホート試験のメタ解析で見つかった点推定値と 1.0 の両者を包含する．その研究では同質であることが明らかになった (I2 = 0%, P = 0.90)．無作為化比較試験の所見からは統計的有意ではないものの，点推定値は効果においてコホート試験と同じ方向を示しており，心血管イベントにおいてはこの無作為化比較試験で差異を評価するには力不足であり，数が少なすぎることを認めざるをえない．

考察

　本系統的レビューとメタ解析は例の仮説を支持する，つまり抗 TNF α 製剤による治療はリウマチ患者の全心血管イベント，心筋梗塞，脳血管疾患のリスク減少と相関していると．リウマチ患者の死因において心血管疾患が 35-50% を占めていることから，この所見は大きな潜在的重要性を有している (20)．全てのコホート試験が示したように，心血管疾患の転帰にもかかわらず，感度分析後も心血管イベントのリスク減少が証明された．更に，累積解析が証明したように，その効果は年余に渡り安定していた．少数の無作為化比較試験しかこの系統的レビューとメタ解析の適合基準に合致しなかったにもかかわらず，点推定値の方向は統計的有意ではなかったものの，リスクを減少させる方向に一致していた．

　コホート試験と無作為化比較試験との所見は一貫性のあるものか，乖離しているか結論付けるべきだろうか？統計的にはそれらは一貫しておらず，それゆえそれらは同じ効果を証明したものと主張される可能性がある．しかしながら，そのコホートの有効性の推定値は有意である一方，無作為化比較試験では有意でない．後者の推定値は 1.0 に近い．Concato らは既に，よくデザインされた観察コホート試験と無作為化比較試験との間の一般的な合同所見の値と関連性について議論している (21)．彼らは次のように提案している．そのようなシナリオはよくあることであり，特異的な曝露効果が関心のある転機について結論するための付加的な堅牢性を提供していると．しかしながら，我々は “healthy user effect” の我々の結果への寄与の可能性について考慮すべきだろう (22)．関節リウマチの文脈においては “healthy user” は一般に若く健康であり，より積極的な（抗 TNF α 製剤を含む）リウマチ管理のようなヘルスサービスを受ける傾向があり，潜在的に他の心血管因子を修飾する治療を受ける傾向にある．これは次のことを暗示している．つまり，患者間の素材の違いがあり，それは抗 TNF α 治療を受けているかそうでないかの違いであり，無作為化比較試験に対して相対的に（コホート試験においては測定不能な交絡因子はコントロール出来ないため）コホート試験における心血管イベント減少の違いとなると．観察試験と無作為化比較試験との間の効果の差異は，ホルモン補充療法の差ではないかとの議論も起きた (23)．しかしホルモン補充療法の記録されたものとは異なり，我々の所見は研究デザインと様々なユーザー層とを超えて一貫していた．抗 TNF α 製剤と心血管イベント発生減少との関連性はヘルスケア分配構造の異なる国家を超えて一貫していた (15, 24)．その効果はまた社会経済的階層を超えて一貫しており，メディケイドを受けるような患者でも抗 TNF α 治療で同じ利益を得ているように見えた (19)．その効果は年齢を超えて一貫しており，若年患者や高齢患者いずれにおいてもイベント発生を減少させていた (14, 16)．最後になるが，我々の累積解析において証明されたように，我々のコホート試験が出版された時期を超えて一貫していた．抗 TNF α 治療がもっと広範囲に処方され，もっと患者集団に拡大することで，我々はその製剤の使用と心血管イベント発生減少との関連を観察し続けた．

　我々のレビューは潜在的に心血管イベントリスクを減少させる原因となる機序を同定していない．疾病管理自体を改善させたり炎症パラメーターを改善させたりしてでも，結果として潜在的に心毒性のある薬物，例えば抗炎症性薬物や副腎皮質ホルモンなど，の使用を減少させている．あるいは抗 TNF α 製剤の直接の効果であって，抗 TNF α 製剤による動脈硬化や炎症の代理マーカーの改善を見ているのかもしれないと基礎科学研究の文脈の中で考慮されるべきである．抗 TNF α 治療は CRP の減少と相関しており，CRP は心血管疾患の独立危険因子として知られている (25, 26)．強直性脊椎炎や他の炎症性疾患の治療は，3ヶ月間の治療後の脂質組成においてエタネルセプトが考慮すべき改善を証明した (27)．血管生物学的研究を通じて Gonzalez-Juanatey とその研究者たちは内皮機能の改善を証明した．それには抗 TNF α を含む生物学的製剤を投与された患者の flow-mediated dilatation または carotid intima-media thickness を測定した (28, 29)．European League Against Rheumatism の最近の推奨では炎症性関節炎に対する早期の積極的治療を強調しており，心血管リスクを2つの経路で低下させる目的で抗 TNF α 製剤とメソトレキセートを使用することを推奨している (30)．1番目の経路とは抗 TNF α 製剤で炎症を減少させることによる直接効果であり，2番目は関節炎と関節機能を改善することで身体活動性が向上し，その後他の心血管リスク因子，例えば糖尿病や高血圧など，を減少させることになる．

　我々の研究には，コホートはそれぞれの治療群に割り付けられ，所定の治療法を受けていると仮定しているという限界がある．DMARDs や何の製剤の治療を受けている患者の割合を考慮した情報が利用できない．我々は次の前提を置くしかなかった，両治療群共に同じく寛解をゴールとして治療を受けていると．我々は抗 TNF α 単独治療群とそれに DMARDs を併用した群とを比較した解析ができなかった．というのはその情報が文献からは提供されなかったためである．メタ回帰分析も出来なかった，重要な併存疾患と心血管リスク因子の情報が限定されていたからである．コホート試験もまた関心のある転帰のモデリングのため統計的に調整を変化させた．コホート試験の結果のメタ解析は限定的で著明に異質であることをも我々は認めた．少なくとも一部では，巨大なサンプルサイズが異質検定には過剰であることを説明しうる．それぞれの研究の効果量の visual inspection は一貫して抗 TNF α 治療でイベントが減少したことを証明しており，故にメタ解析は効果が均一な方向と判断されたと考えられている．

　抗 TNF α による無作為化比較試験に関する限界は，抗 TNF α 治療による短期治療効果を第 1 に実施しており，副作用は secondary end point となっていることによる．無作為化比較試験は高度に選択された集団からなり，心血管イベントリスクが低いように見える．無作為化比較試験を我々の研究に含めた利点は，副作用が厳しい基準で判定される点にあり，転帰の提供が確実であることであった．それらはまた抗 TNF α 治療と標準的な DMARDs 治療との効果を直接比較することを可能にした．

　我々のレビュー所見についての最後の注意点として，certolizmab が我々の研究では考慮されていないことである．Certolizmab は承認されたばかりであり，我々のレビュー開始時には臨床現場に広がり始めたばかりであり，我々の検索方法には先験的に含まれていなかった．我々の適合基準に合致する certolizmab の研究は1つだけであり (31)，この報告には我々のメタ解析にインパクトを与える結果はなかった．

　要約すると，我々は次のことを同定した，抗 TNF α 製剤による関節リウマチの治療は心血管イベントリスク減少に関連しているようで，その所見は明らかな生物学的なもっともらしさを支持している．我々は，リウマチにおける抗 TNF α 製剤の利益の更なる観察に努めた，特に無作為化比較試験とコホートの両者においてより長期間観察したものを．より長期間観察すれば，心血管イベント減少効果をより顕著に観察でき，抗 TNF α 治療を現在受けている患者は相対的に若く，数年後に心血管疾患に罹患することはなくなるかも知れない．潜在的な共同設立者がより詳細な情報を提供する研究により，この文献本体により高い価値を付加することになるだろう．

Probability density function, expected value and variance of each probability distribution

I’d like to summarize probability density function (f(x)), expected value (E(X)) and variance (V(X)) of following probability distribution.

Supergeometric distribution  
\displaystyle f(x) = \frac{{}_{M}C_x\cdot{}_{N-M}C_{n-x}}{{}_{N}C_{n}} \displaystyle x = Max(0, n - (N - M)), \cdots, Min(n, M)
\displaystyle E(X) = np \displaystyle p = \frac{M}{N}
\displaystyle V(X) = np(1 - p)\frac{N - n}{N - 1}  
Binomial distribution  
\displaystyle f(x) = {}_{n}C_{x}p^{x}(1 - p)^{n - x} \displaystyle x = 0, 1, \cdots, n
\displaystyle E(X) = np \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = np(1 - p)  
Poisson distribution  
\displaystyle f(x) = \frac{\exp(- \lambda)\cdot\lambda^x}{x!} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \lambda \lambda = np
\displaystyle V(X) = \lambda
Geometric distribution  
\displaystyle f(x) = p(1 - p)^{x - 1} \displaystyle x = 1, 2, 3, \cdots
\displaystyle E(X) = \frac{1}{p} \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = \frac{1 - p}{p^2}  
Negative binomial distribution  
\displaystyle f(x) = {}_{k + x - 1}C_{x}p^{k}(1-p)^{x} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \frac{k(1 - p)}{p}  
\displaystyle V(X) = \frac{k(1 - p)}{p^2}  
Normal distribution  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x - m)^2}{2\sigma^2}\right) \displaystyle - \infty < x < \infty[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = m  
\displaystyle V(X) = \sigma^2 \displaystyle \sigma > 0
Exponential distribution  
\displaystyle f(x) = \lambda\exp(-\lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{1}{\lambda}  
\displaystyle V(X) = \frac{1}{\lambda^2}  
Gamma distribution  
\displaystyle f(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha - 1}\exp(- \lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{\alpha}{\lambda} \displaystyle \lambda, \alpha > 0
\displaystyle V(X) = \frac{\alpha}{\lambda^2}  
Beta distribution  
\displaystyle f(x) = \frac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{B(\alpha, \beta)} \displaystyle 0 < x < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle f(x) = 0 \displaystyle x \le 0, 1 \le x
\displaystyle E(X) = \frac{\alpha}{\alpha + \beta}  
\displaystyle V(X) = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}  
Cauchy distribution  
\displaystyle f(x) = \frac{\alpha}{\pi(\alpha^2 + (x - \lambda)^2)} \displaystyle \alpha > 0
Log-normal distribution  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma x}\exp\left(-\frac{(\log(x) - m)^2}{2\sigma^2}\right) \displaystyle x > 0
\displaystyle f(x) = 0 \displaystyle x \le 0
\displaystyle E(X) = \exp\left(m + \frac{\sigma^2}{2}\right) \displaystyle \sigma > 0
\displaystyle V(X) = \exp[2m + \sigma^2](\exp[\sigma^2] - 1)  
Pareto distribution  
\displaystyle f(x) = \frac{x_0^\alpha}{x^{\alpha + 1}} \displaystyle x \ge x_0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{ax_0}{a - 1} \displaystyle a > 1
\displaystyle V(X) = \frac{ax_0^2}{a - 2} - \left(\frac{ax_0}{a - 1}\right)^2 \displaystyle a > 2
Weibull distribution  
\displaystyle f(x) = \frac{\gamma x^{\gamma - 1}}{\lambda^b}\exp\left[-\left(\frac{x}{y}\right)^\gamma\right] \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \lambda\Gamma\left(1 + \frac{1}{\gamma}\right) \displaystyle \lambda > 0
\displaystyle V(X) = \lambda^2\left[\Gamma\left(2 + \frac{1}{\gamma}\right) - \left(\Gamma\left(1 + \frac{1}{\gamma}\right)\right)^2\right] \displaystyle \gamma > 0

確率分布ごとの確率密度関数および期待値と分散

　確率分布ごとの確率密度関数 f(x), 確率変数 X の期待値 E(X) および分散 V(X) をまとめました．

超幾何分布  
\displaystyle f(x) = \frac{{}_{M}C_x\cdot{}_{N-M}C_{n-x}}{{}_{N}C_{n}} \displaystyle x = Max(0, n - (N - M)), \cdots, Min(n, M)
\displaystyle E(X) = np \displaystyle p = \frac{M}{N}
\displaystyle V(X) = np(1 - p)\frac{N - n}{N - 1}  
二項分布  
\displaystyle f(x) = {}_{n}C_{x}p^{x}(1 - p)^{n - x} \displaystyle x = 0, 1, \cdots, n
\displaystyle E(X) = np \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = np(1 - p)  
ポアソン分布  
\displaystyle f(x) = \frac{\exp(- \lambda)\cdot\lambda^x}{x!} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \lambda \lambda = np
\displaystyle V(X) = \lambda
幾何分布  
\displaystyle f(x) = p(1 - p)^{x - 1} \displaystyle x = 1, 2, 3, \cdots
\displaystyle E(X) = \frac{1}{p} \displaystyle 0 < p < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle V(X) = \frac{1 - p}{p^2}  
負の二項分布  
\displaystyle f(x) = {}_{k + x - 1}C_{x}p^{k}(1-p)^{x} \displaystyle x = 0, 1, 2, \cdots
\displaystyle E(X) = \frac{k(1 - p)}{p}  
\displaystyle V(X) = \frac{k(1 - p)}{p^2}  
正規分布  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x - m)^2}{2\sigma^2}\right) \displaystyle - \infty < x < \infty[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = m  
\displaystyle V(X) = \sigma^2 \displaystyle \sigma > 0
指数分布  
\displaystyle f(x) = \lambda\exp(-\lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{1}{\lambda}  
\displaystyle V(X) = \frac{1}{\lambda^2}  
ガンマ分布  
\displaystyle f(x) = \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha - 1}\exp(- \lambda x) \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{\alpha}{\lambda} \displaystyle \lambda, \alpha > 0
\displaystyle V(X) = \frac{\alpha}{\lambda^2}  
ベータ分布  
\displaystyle f(x) = \frac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{B(\alpha, \beta)} \displaystyle 0 < x < 1[/latex]</td> </tr> <tr> <td>[latex]\displaystyle f(x) = 0 \displaystyle x \le 0, 1 \le x
\displaystyle E(X) = \frac{\alpha}{\alpha + \beta}  
\displaystyle V(X) = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}  
コーシー分布  
\displaystyle f(x) = \frac{\alpha}{\pi(\alpha^2 + (x - \lambda)^2)} \displaystyle \alpha > 0
対数正規分布  
\displaystyle f(x) = \frac{1}{\sqrt{2\pi}\sigma x}\exp\left(-\frac{(\log(x) - m)^2}{2\sigma^2}\right) \displaystyle x > 0
\displaystyle f(x) = 0 \displaystyle x \le 0
\displaystyle E(X) = \exp\left(m + \frac{\sigma^2}{2}\right) \displaystyle \sigma > 0
\displaystyle V(X) = \exp[2m + \sigma^2](\exp[\sigma^2] - 1)  
パレート分布  
\displaystyle f(x) = \frac{x_0^\alpha}{x^{\alpha + 1}} \displaystyle x \ge x_0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \frac{ax_0}{a - 1} \displaystyle a > 1
\displaystyle V(X) = \frac{ax_0^2}{a - 2} - \left(\frac{ax_0}{a - 1}\right)^2 \displaystyle a > 2
ワイブル分布  
\displaystyle f(x) = \frac{\gamma x^{\gamma - 1}}{\lambda^b}\exp\left[-\left(\frac{x}{y}\right)^\gamma\right] \displaystyle x \ge 0
\displaystyle f(x) = 0 \displaystyle x < 0[/latex]</td> </tr> <tr> <td>[latex]\displaystyle E(X) = \lambda\Gamma\left(1 + \frac{1}{\gamma}\right) \displaystyle \lambda > 0
\displaystyle V(X) = \lambda^2\left[\Gamma\left(2 + \frac{1}{\gamma}\right) - \left(\Gamma\left(1 + \frac{1}{\gamma}\right)\right)^2\right] \displaystyle \gamma > 0

How to calculate required sample size in chi-square test, Fisher exact test, Student’s t-test and log-rank test?

Sample size calculation may be hard for research member, because it’s difficult to distinguish sample size is enough or not when it was not statistical significant. Required sample size calculation is very important.

χ2 test without correction

To compare survival rate between risk/intervention group and control group, it’s required to execute χ2 test. You can calculate sample size as following formula. With significance level (α) 0.05 (two-tailed) and statistical power (1 – β) 0.8 (one-sided), Zα/2 is 1.96 and Zβ is 0.84, respectively.

\displaystyle N_0 = \frac{\left(Z_{\alpha/2}\sqrt{(1+\phi)\bar{p}(1 - \bar{p})} + Z_\beta\sqrt{\phi p_0(1 - p_0) + p_1(1 - p_1)}\right)^2}{\phi\delta^2}

\displaystyle N_1 = \phi N_0

If effect size δ was expressed with odd ratio (OR), sample size could be calculated as formula below.

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_\beta)^2}{(\log{OR})^2\bar{p}(1 - \bar{p})}

\displaystyle N_1 = \phi N_0

\displaystyle N_0 : required number of control group.

\displaystyle N_1 : required number of risk/intervention group.

\displaystyle n_0 : actual number of control group.

\displaystyle n_1 : actual number of risk/intervention group.

\displaystyle \phi = \frac{n_1}{n_0}: the ratio of number of risk/intervention group to number of control group.

\displaystyle p_0 : survival rate or efficacy in control group.

\displaystyle p_1 : survival rate or efficacy in risk/intervention group.

\displaystyle \delta = p_1 - p_0 : effect size, difference between two groups.

\displaystyle \bar{p} = \frac{p_0 + \phi p_1}{1 + \phi}

χ2 test with Yates correction and Fisher exact test

When you execute χ2 test with Yates correction or Fisher exact test, you have to correct N0 with multiplying by C, correction term as below.

\displaystyle C = \frac{1}{4}\left(1 + \sqrt{1 + \frac{2 (1 + \phi)}{\phi N_0 |\delta|}}\right)^2

Student’s t-test

In Student’s t-test, you have to calculate standardized effect size (Δ) first with a mean of control group and a mean of risk/intervention group. Then you can calculate sample size with Δ as below. It’s assumed that the variances are equal between control group and risk/intervention group.

\displaystyle \Delta = \frac{|\mu_0 - \mu_1|}{\sigma}

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_{\beta})^2}{\Delta^2} + \frac{Z_{\alpha/2}^2}{2(1 + \phi)}

\displaystyle N_1 = \phi N_0

log-rank test

In log-rank test, you can calculate required number of event (e) and sample size (N) as following formula. p0 and p1 are cumulative survival rate of control group and risk/intervention group, respectively, derived from previous research or cumulative survival rate after 1 or 2 years from the research started. When φ was 1, it means equal sample size in both groups, it would bring same result as described in How to calculate appropriate sample size in Cox proportional hazard analysis with cross tabulation?.

\displaystyle \theta = \frac{\log(p_1)}{\log(p_0)}

\displaystyle e_0 = \frac{1}{(1 + \phi)\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e_1 = \phi e_0 = \frac{1}{1 + \phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e = e_0 + e_1 = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle N_0 = \frac{e}{(1 - p_0) + \phi(1 - p_1)} = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_1 = \phi N_0

\displaystyle N = N_0 + N_1 = \frac{1 + \phi}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_0 : required number of control group.

\displaystyle N_1 : required number of risk/intervention group.

\displaystyle n_0 : actual number of control group.

\displaystyle n_1 : actual number of risk/intervention group.

\displaystyle \phi = \frac{n_1}{n_0} : the ratio of number of risk/intervention group to number of control group.

\displaystyle p_0 : survival rate or efficacy of control group.

\displaystyle p_1 : survival rate or efficacy of risk/intervention group.

References:
TABLES OF THE NUMBER OF PATIENTS REQUIRED IN CLINICAL TRIALS USING THE LOG RANK TEST

χ2乗検定，Fisher正確確率検定，Student t検定およびlog-rank検定においてサンプルサイズを計算するには

　サンプルサイズの計算は重要です．多くの研究者にとって統計的有意差が出なかった場合に，それがサンプルサイズ不足が原因によるものかどうかの判断ができないからです．全ての検定を網羅することはできませんでしたが，重要と思われる主な検定においてサンプルサイズを計算する方法を述べます．

χ2検定

　リスク群・介入群と対照群との2群間で有効率・生存率を比較するにはχ2乗検定を行いますが，その際のサンプルサイズの算出には下記の式を用います．α = 0.05 （両側）, 1 – β = 0.8 （片側）とすると Zα/2 = 1.96, Zβ = 0.84 として計算します．

\displaystyle N_0 = \frac{\left(Z_{\alpha/2}\sqrt{(1+\phi)\bar{p}(1 - \bar{p})} + Z_\beta\sqrt{\phi p_0(1 - p_0) + p_1(1 - p_1)}\right)^2}{\phi\delta^2}

\displaystyle N_1 = \phi N_0

　効果量 δ がオッズ比で表現できる場合，サンプルサイズは下式で求まります．

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_\beta)^2}{(\log{OR})^2\bar{p}(1 - \bar{p})}

\displaystyle N_1 = \phi N_0

\displaystyle N_0 : 対照群に必要なサンプルサイズ

\displaystyle N_1 : リスク群・介入群に必要なサンプルサイズ

\displaystyle n_0 : 対照群の実際の症例数

\displaystyle n_1 : リスク群・介入群の実際の症例数

\displaystyle \phi = \frac{n_1}{n_0}

\displaystyle p_0 : 対照群の有効率・生存率

\displaystyle p_1 : リスク群・介入群の有効率・生存率

\displaystyle \delta = p_1 - p_0 : リスク群・介入群と対照群との有効率・生存率の差

\displaystyle \bar{p} = \frac{p_0 + \phi p_1}{1 + \phi}

Yates補正による χ2 検定と Fisher 正確確率検定

　Yates 補正や Fisher 正確確率検定の際には N0 に補正項 C を乗じて補正する必要があります．リンクした書籍には平方根内の項に 1 を加算していますが，森實敏夫の教科書には加算していません．しかしウェブ上のサンプルサイズの計算の数式は合っています．

\displaystyle C = \frac{1}{4}\left(1 + \sqrt{1 + \frac{2 (1 + \phi)}{\phi N_0 |\delta|}}\right)^2

Student t 検定

　対照群の平均値 μ0 およびリスク群・介入群の平均値 μ1 から効果量 Δ を計算し，そこからサンプルサイズを求めます．この場合，対照群とリスク群・介入群とでは分散が等しいと仮定しています．

\displaystyle \Delta = \frac{|\mu_0 - \mu_1|}{\sigma}

\displaystyle N_0 = \left(\frac{1 + \phi}{\phi}\right)\frac{(Z_{\alpha/2} + Z_{\beta})^2}{\Delta^2} + \frac{Z_{\alpha/2}^2}{2(1 + \phi)}

\displaystyle N_1 = \phi N_0

log-rank 検定

　log-rank 検定において必要なイベント数 e およびサンプルサイズ N は Freedman の方法で下式にて求まります．p0 および p1 は先行研究や試験開始後 1－2 年での累積生存率です．φ = 1 の場合，COX比例ハザードモデルのlog-rank検定に必要なサンプルサイズを四分表から計算するで説明した数式と同じ結果になります．

　森實敏夫の教科書の記載には誤りがあります．イベント数 e を求める式の分母において，Freedman の原著では φ は括弧の外にありますが，森實敏夫の教科書の記載では括弧内にあります．ウェブ上のサンプルサイズの計算の数式は合っています．参考文献の Freedman の原著は有料です．

\displaystyle \theta = \frac{\log(p_1)}{\log(p_0)}

\displaystyle e_0 = \frac{1}{(1 + \phi)\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e_1 = \phi e_0 = \frac{1}{1 + \phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle e = e_0 + e_1 = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2(Z_{\alpha/2} + Z_\beta)^2

\displaystyle N_0 = \frac{e}{(1 - p_0) + \phi(1 - p_1)} = \frac{1}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_1 = \phi N_0

\displaystyle N = N_0 + N_1 = \frac{1 + \phi}{\phi}\left(\frac{1 + \phi\theta}{1 - \theta}\right)^2\frac{(Z_{\alpha/2} + Z_\beta)^2}{(1 - p_0) + \phi(1 - p_1)}

\displaystyle N_0 : 対照群に必要なサンプルサイズ

\displaystyle N_1 : リスク群・介入群に必要なサンプルサイズ

\displaystyle n_0 : 対照群の実際の症例数

\displaystyle n_1 : リスク群・介入群の実際の症例数

\displaystyle \phi = \frac{n_1}{n_0} : リスク群・介入群の症例数と対照群の症例数との比

\displaystyle p_0 : 対照群の有効率・生存率

\displaystyle p_1 : リスク群・介入群の有効率・生存率

参考文献：
TABLES OF THE NUMBER OF PATIENTS REQUIRED IN CLINICAL TRIALS USING THE LOG RANK TEST