Mathematics | Improve Society

Maxima and minima

If for all x such that |x – a| < δ where f(x) ≤ f(a) [ or f(x) ≥ f(a)], f(a) is a relative maximam [ or relative minimum]. For f(x) to have a relative maximum or minimum at x = a, it must have f'(a) = 0. Then if f”(a) < 0 it is a relative maximum while if f”(a) ≥ 0 it is a relative minimum. Possible points at which f(x) has a relative maxima or minima are obtained by solving f'(x) = 0, i.e. by finding the values of x where the slope of the graph f(x) is equal to zero.

Similarly f(x, y) has a relative maximum or minimum at x = a, y = b if f_x(a, b) = 0, f_y(a, b) = 0. Thus possible points at which f(x, y) has relative maxima or minima are obtained by solving simultaneously the equations
$\displaystyle \frac{\partial f}{\partial x} = 0,\ \frac{\partial f}{\partial y} = 0$
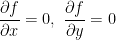
Extensions to functions of more than two variables are similar.

極大と極小

　全ての x について |x – a| < δ であり，また f(x) ≤ f(a) （または f(x) ≥ f(a)）である時，f(a) は極大（または極小）であると言います．

　f(x) が x = a において極大または極小を持つには f'(a) = 0 でなくてはなりません．もし f”(a) < 0 ならそれは極大であり，一方もし f”(a) > 0 ならそれは極小です．f(x) において極大または極小となる可能性のある点は f'(x) = 0 を解くこと，例えば， f(x) のグラフの傾きがゼロと等しくなる x の値を見つけることで得られます．

　同様に f_x(a, b) = 0, f_y(a, b) = 0 ならば f(x, y) は x = a, y = b において極大または極小を持ちます．故に f(x, y) f(x, y) で極大または極小をもつ可能性のある点は，同様に次の方程式を解くことで得られます．

$\displaystyle \frac{\partial f}{\partial x} = 0,\ \frac{\partial f}{\partial y} = 0$

　2 変数以上の関数への拡張も同様です．

Linear equations and determinants

$\displaystyle a_1x + b_1y = c_1\\\vspace{0.2 in} a_2x + b_2y = c_2\ \cdots(1)$
These represent two lines in the xy plane, and in general will meet in a point whose coordinates (x, y) are found by solving simultaneously.
$\displaystyle x = \frac{c_1b_2 - b_1c_2}{a_1b_2 - b_1a_2},\ y = \frac{a_1c_2 - c_1a_2}{a_1b_2 - b_1a_2}\ \cdots(2)$
It’s convenient to write these in determinant form as
$\displaystyle x = \frac{\left|\begin{array}{cc}c_1 & b_1 \\ c_2 & b_2\end{array}\right|}{\left|\begin{array}{cc}a_1 & b_1 \\ a_2 & b_2\end{array}\right|},\ y = \frac{\left|\begin{array}{cc}a_1 & c_1 \\ a_2 & c_2\end{array}\right|}{\left|\begin{array}{cc}a_1 & b_1 \\ a_2 & b_2 \end{array}\right|}\ \cdots(3)$
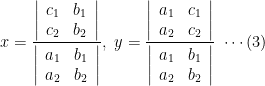
where it is defined a determinant of the second order or order 2 to be
$\displaystyle \left|\begin{array}{cc}a & b \\ c & d \end{array}\right| = ad - bc\ \cdots(4)$
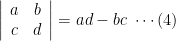
It should be noted that the denominator for x and y in (3) is the determinant consisting of the coefficients of x and y in (1). The numerator for x is found by replacing the first column of the denominator by the constants c₁, c₂ on the right side of (1). Similarly the numerator for y is found by replacing the second column of the denominator by c₁, c₂. This procedure is often called Cramer’s rule. In case the denominator in (3) is zero, the two lines represented by (1) do not meet in one point but are either coincident or parallel.

The ideas are easily extended. Thus you can consider the equations
$\displaystyle a_1x + b_1y + c_1z = d_1\\\vspace{0.2 in} a_2x + b_2y + c_2z = d_2\ \cdots(5)\\\vspace{0.2 in} a_3x + b_3y + c_3z = d_3$
representing 3 planes. If they intersect in a point, the coordinates (x, y, x) of this point are found from Cramer’s rule to be
$\displaystyle x = \frac{\left|\begin{array}{ccc}d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|},\ y = \frac{\left|\begin{array}{ccc}a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|},\ z = \frac{\left|\begin{array}{ccc}a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|}\ \cdots(6)$
where it can be defined the determinant of order 3 by
$\displaystyle \left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\a_3 & b_3 & c_3\end{array}\right| = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 - (b_1a_2c_3 + a_1c_2b_3 + c_1b_2a_3)\ \cdots(7)$
The determinant can also be evaluated in terms of second order determinants as follows
$\displaystyle a_1\left|\begin{array}{cc}b_2 & c_2 \\ b_3 & c_3\end{array}\right| - b_1\left|\begin{array}{cc}a_2 & c_2 \\ a_3 & c_3\end{array}\right| + c_1\left|\begin{array}{cc}a_2 & b_2 \\ a_3 & b_3\end{array}\right|\ \cdots(8)$
where it is noted that a₁, b₁, c₁ are the elements in the first row and the corresponding second order determinants are those obtained from the given third order determinant by removing the row and column in which the element appears.

一次方程式と行列式

$\displaystyle a_1x + b_1y = c_1\\\vspace{0.2 in} a_2x + b_2y = c_2\ \cdots(1)$

　これらは xy 平面における 2 本の直線を示しており，一般に (x, y) 座標で交わる 1 点において同時に解が得られます．

$\displaystyle x = \frac{c_1b_2 - b_1c_2}{a_1b_2 - b_1a_2},\ y = \frac{a_1c_2 - c_1a_2}{a_1b_2 - b_1a_2}\ \cdots(2)$

　これを行列式で表現するのは便利です．

$\displaystyle x = \frac{\left|\begin{array}{cc}c_1 & b_1 \\ c_2 & b_2\end{array}\right|}{\left|\begin{array}{cc}a_1 & b_1 \\ a_2 & b_2\end{array}\right|},\ y = \frac{\left|\begin{array}{cc}a_1 & c_1 \\ a_2 & c_2\end{array}\right|}{\left|\begin{array}{cc}a_1 & b_1 \\ a_2 & b_2 \end{array}\right|}\ \cdots(3)$

　2 次の行列式は次のように定義します．

$\displaystyle \left|\begin{array}{cc}a & b \\ c & d \end{array}\right| = ad - bc\ \cdots(4)$

　強調すべきことですが，(3) で記述した x と y の分母は (1) の x と y の係数を含む行列式です．x の分子は分母の 1 列目を (1) の右側の c₁, c₂ の定数で置換して得られます．同様に y の分子は c₁, c₂ で 2 列目を置換して得られます．この処理はしばしば Crame’s rule と呼ばれます．(3) の分母がゼロの場合は (1) で示される 2 行は1点で交差せず，一致するか平行であるかです．

　この考えは容易に拡張できます．次の方程式を考えてみましょう．

$\displaystyle a_1x + b_1y + c_1z = d_1\\\vspace{0.2 in} a_2x + b_2y + c_2z = d_2\ \cdots(5)\\\vspace{0.2 in} a_3x + b_3y + c_3z = d_3$

3行を示します．これらが 1 点で交わる場合，この点の (x, y, z) 座標は Cramer’s rule から得られます．

$\displaystyle x = \frac{\left|\begin{array}{ccc}d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|},\ y = \frac{\left|\begin{array}{ccc}a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|},\ z = \frac{\left|\begin{array}{ccc}a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3\end{array}\right|}{\left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{array}\right|}\ \cdots(6)$

　3 次の行列式は次のように定義されます．

$\displaystyle \left|\begin{array}{ccc}a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\a_3 & b_3 & c_3\end{array}\right| = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 - (b_1a_2c_3 + a_1c_2b_3 + c_1b_2a_3)\ \cdots(7)$

　この行列式は 2 次の行列式の面で次のように評価されます．

$\displaystyle a_1\left|\begin{array}{cc}b_2 & c_2 \\ b_3 & c_3\end{array}\right| - b_1\left|\begin{array}{cc}a_2 & c_2 \\ a_3 & c_3\end{array}\right| + c_1\left|\begin{array}{cc}a_2 & b_2 \\ a_3 & b_3\end{array}\right|\ \cdots(8)$

　ここで強調しておきたいことは，a₁, b₁, c₁ は 1 行目の要素であり，対応する 2 次の行列式は 3 次の行列式からその要素が現れる行と列を除去して得られます．

Taylor series for functions of two or more variables

The ideas involved in Taylor series for functions of one variable can be generalized. For example, the Taylor series for $f(x, y)$ about x = a, y = b can be written
$\displaystyle f(x, y) = f(a, b) + f_x(a, b)(x -a) + f_y(a, b)(y -b)\\\vspace{0.2 in} \ \ \ + \frac{1}{2!}\big[f_{xx}(a, b)(x - a)^2 + 2f_{xy}(a, b)(x - a)(y - b) + f_{yy}(a, b)(y - b)^2\big] + \cdots$

2変数以上の関数のテーラー級数

　1 変数関数のテーラー級数に関する考えは一般化可能です．例えば， $f(x, y$ の x = a, y = b におけるテーラー級数は下記のように記述できます．

$\displaystyle f(x, y) = f(a, b) + f_x(a, b)(x -a) + f_y(a, b)(y -b)\\\vspace{0.2 in} \ \ \ + \frac{1}{2!}\big[f_{xx}(a, b)(x - a)^2 + 2f_{xy}(a, b)(x - a)(y - b) + f_{yy}(a, b)(y - b)^2\big] + \cdots$

Partial derivatives

The partial derivatives of $f(x, y)$ with respect to x and y are defined by
$\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}$
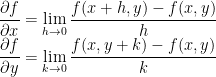
if these limits exist. It’s often written h = Δx, k = Δy. Note that $\partial f/\partial x$ is simply the ordinary derivative of f with respect to x keeping y constant, while $\partial f/\partial y$ is the ordinary derivative of f with respect to y keeping x constant.

Higher derivatives are defined similarly. For example, you have the second order derivatives
$\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}$
The deviation are sometimes denoted f_x and f_y. In such case f_x(a, b), f_y(a, b) denote these partial derivatives evaluated at (a, b).

The deviations are denoted by f_xx, f_xy, f_yx, f_yy respectively. The second and third results will be the same if f has continuous partial derivatives of second order at least.

The differentiation of f(x, y) is defined as
$\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$
where h = Δx = dx, k = Δy = dy.

偏微分

　x および y に対しての $f(x, y)$ の偏導関数は次式で定義されます．

$\displaystyle \frac{\partial f}{\partial x}= \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x, y)}{h}\\\vspace{0.2 in} \frac{\partial f}{\partial y} = \lim\limits_{k \rightarrow 0} \frac{f(x, y + k) - f(x, y)}{k}$

　しばしば h = Δx, k = Δy のように記述します．y を定数とした x に対する f の通常の導関数は単に $\partial f/\partial x$ と記述し，一方 x を定数とした y に対する f の通常の導関数は $\partial f/\partial y$ と記述します．

　高階の導関数もまた同様に定義します．例えば，2 階の通常の導関数は下記のようです．

$\displaystyle \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial x^2}\\\vspace{0.2 in} \frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial x\partial y}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) = \frac{\partial^2f}{\partial y\partial x}\\\vspace{0.2 in} \frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) = \frac{\partial^2f}{\partial y^2}$

　偏導関数は時々 f_x や f_y とも記述します．そのような場合 f_x(a, b), f_y(a, b) は点 (a, b) において評価されるこれらの偏微分です．

　偏導関数はまた f_xx, f_xy, f_yx, f_yy とも記述します．f が少なくとも 2 階の連続な偏微分を有するなら 2 階や 3 階微分の結果もまた同様です．

　 $f(x, y)$ の全微分は次のように定義します．

$\displaystyle df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy$

　ただし h = Δx = dx, k = Δy = dy です．

Functions of two or more variables

The concept of function of one variable can be extended to functions of two or more variables. Thus for example $z = f(x, y)$ defines a function f which assigns to the number pair (x, y) the number z.

It’s familiar for some people with graphing $z = f(x, y)$ in a 3-dimensional xyz coordinate system to obtain a surface. Sometime x and y are called independent variables and z a dependent variable. Occasionally it’s written $z = z(x, y)$ rather than $z = f(x, y)$ , using the system z in two different senses. however, no confusion should result.

The ideas of limits and continuity for functions of two or more variables pattern closely those for one variable.

2変数以上の関数

　1 変数関数の概念は 2 変数以上の関数にも拡張可能です．それゆえ例えば $z = f(x, y)$ は 2 つの数 (x, y) を 1 つの数 z に割り付ける関数 f を定義するものです．

　ある人にとっては $z = f(x, y)$ を xyz 座標軸系の 3 次元にグラフ化して面を得ることは馴染み深いでしょう．時には x と y は独立変数と呼ばれ，z は従属変数と呼ばれます．まれに $z = f(x, y)$ ではなく $z = z(x, y)$ と記述されることがあり，z 系は異なる意味で用いられます．しかし混同すべきではありません．

　2 変数以上の関数の極限と連続性の概念は 1 変数のそれに近いです．

Taylor series

The Taylor series for f(x) about x = a is defined as

$\displaystyle f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)(x - a)^2}{2!} + \cdots + \frac{f^{n -1}(a)(x - a)^{n-1}}{(n -1)!} + R_n$ (a)
where $\displaystyle R_n = \frac{f^n(x - n)^n}{n!}$ , x₀ between a and x.(b)
is called the reminder and where it is supposed that f(x) has derivatives of order n at least. The case where n = 1 is often called law of the mean or mean-value theorem and can be written as
$\displaystyle \frac{f(x) -f(a)}{x - a} = f'(x_0)$ , x₀ between a and x (c)

The infinite series corresponding to (a), also called the formal Taylor series for f(x), will converge in some interval if $\lim\limits_{n \rightarrow \infty}R_n = 0$ in this interval. Some important Taylor series together with their intervals of convergence are as follows.

$\displaystyle e^n = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} +\frac{x^4}{4!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \ln(1 + x) = x - \frac{x^2}{2!} + \frac{x^3}{3!} - \frac{x^4}{4!} + \cdots\ -1 < x \le 1[/latex]</li> <li>[latex]\displaystyle \tan^{-1}x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -1 \le x \le 1$

A series of the form $\sum_{n=0}^{\infty}c_n(x - a)^n$ is often called a power series. Such power series are uniformly convergent in any interval which lies entirely within the interval of convergence.

テーラー級数

　x = a における f(x) のテーラー級数は下記のように定義されます．

$\displaystyle f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)(x - a)^2}{2!} + \cdots + \frac{f^{n -1}(a)(x - a)^{n-1}}{(n -1)!} + R_n$ (a)
ここで $\displaystyle R_n = \frac{f^n(x - n)^n}{n!}$ , x₀ は a と x の範囲内(b)
は reminder と呼ばれ， f(x) が最低でも n 次の微分係数を持つと想定します．n = 1 の場合は特に平均の法則または平均値の定理と呼ばれ，次のように記述します．
$\displaystyle \frac{f(x) -f(a)}{x - a} = f'(x_0)$ , x₀ は a と x の範囲内(c)

　(a) に対応した無限級数は f(x) の正規テーラー級数とも呼ばれ，必ずある区間に収束します．仮に $\lim\limits_{n \rightarrow \infty}R_n = 0$ がこの区間にあるなら．いくつかの重要なテーラー級数と収束値をその区間とともに示します．

$\displaystyle e^n = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} +\frac{x^4}{4!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots\ -\infty < x < \infty[/latex]</li> <li>[latex]\displaystyle \ln(1 + x) = x - \frac{x^2}{2!} + \frac{x^3}{3!} - \frac{x^4}{4!} + \cdots\ -1 < x \le 1[/latex]</li> <li>[latex]\displaystyle \tan^{-1}x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\ -1 \le x \le 1$

　ある形の級数 $\sum_{n=0}^{\infty}c_n(x - a)^n$ はしばしばべき級数と呼ばれます．そのようなべき級数はどの区間にも一様収束し，それは収束区間内全体にあります．

Uniform convergence

The ideas of previous article can be extended to the case where the u_n are functions of x denoted by u_n(x). In such case the sequences or series will converge of diverge according to the particular value of x. The set of values of x for which a sequence or series converges is called the region of convergence, denoted $\cal R$ .

The series u₁(x) + u₂(x) + … converges to the sum S(x) in a region $\cal R$ if given ε > 0 there exists a number N, which in general depends on both ε and x, such that |S(x) – S_n(x)| < ε whenever n > N where S_n(x) = u₁(x) + … + u_n(x). If you can find N depending only on ε and not on x, the series converges uniformly to S(x) in $\cal R$ . Uniformly convergent series have many important advantages as indicated in the following theorems.

If u_n(x), n = 1, 2, 3, … are continuous in a ≤ x ≤ b and ∑ u_n(x) is uniformly convergent to S(x) in a ≤ x ≤ b, then S(x) is continuous in a ≤ x ≤ b.

If ∑u(x) converges uniformly to S(x) in a ≤ x ≤ b and u_n(x), n = 1, 2, 3, … are integrable in a ≤ x ≤ b, then
$\displaystyle \int^{b}_{a}S(x)dx = \int^{b}_{a}(u_1(x) + u_2(x) + \cdots)dx = \int^{b}_{a}u_1(x)dx + \int^{b}_{a}u_2(x)dx + \cdots$

If u_n(x), n = 1, 2, 3, … are continuous and have continuous derivatives in a ≤ x ≤ b and if ∑u_n(x) converges to S(x) while ∑u’_n(x) is uniformly convergent in a ≤ x ≤ b, then
$\displaystyle S'(x) = \frac{d}{dx}(u_1(x) + u_2(x) + \cdots) = u'_1(x) + u'_2(x) + \cdots$

If there is aset of positive constants M_n, n = 1, 2, 3, … such that |u_n| ≤ M_n in $\cal R$ and ∑M_n converges, then ∑u_n(x) is uniformly convergent [and also absolutely convergent] in $\cal R$ .

An important test for uniform convergence, often called the Weierstrass M test, is given by the above.

一様収束

　前回の記事で述べた考えは u_n が x の関数の場合，u_n(x) と記述するが，に拡張できます．そのような場合，数列または級数が収束するか発散するかは x の特定の値に依存します．数列や級数が収束する x の値の集合は収束領域と呼ばれ， $\cal R$ と表記します．

　級数 u₁(x) + u₂(x) + … は領域 $\cal R$ 内の S(x) の合計に収束します，もし ε > 0 があってε と x の両者に依存するある数 N があり，|S(x) – S_n(x)| < ε を満たし，常に n > N であって S_n(x) = u₁(x) + … + u_n(x) の場合には．もし ε のみに依存し，x には依存しない N を見つけられるなら，その級数は $\cal R$ 内の S(x) に一様収束します．一様収束級数には次の定理に示すように多くの利点があります．

仮に u_n(x), n = 1, 2, 3, … が a ≤ x ≤ b の範囲で連続であり，かつ ∑ u_n(x) が a ≤ x ≤ b の範囲で S(x) に一様収束するなら S(x) は a ≤ x ≤ b の範囲で連続である．
仮に ∑u(x) が S(x) に a ≤ x ≤ b の範囲で一様収束し，かつ u_n(x), n = 1, 2, 3, … が a ≤ x ≤ b の範囲で積分可能である場合は以下が成り立つ．
$\displaystyle \int^{b}_{a}S(x)dx = \int^{b}_{a}(u_1(x) + u_2(x) + \cdots)dx = \int^{b}_{a}u_1(x)dx + \int^{b}_{a}u_2(x)dx + \cdots$
仮に u_n(x), n = 1, 2, 3, … が連続でかつ a ≤ x ≤ b の範囲で連続して微分可能であり，さらに ∑u_n(x) が S(x) に収束し，∑u’_n(x) が a ≤ x ≤ b の範囲で一様収束するなら以下が成り立つ．
$\displaystyle S'(x) = \frac{d}{dx}(u_1(x) + u_2(x) + \cdots) = u'_1(x) + u'_2(x) + \cdots$
正の定数 M_n が存在し n = 1, 2, 3, … で $\cal R$ 領域内の M_n において |u_n| ≤ M_n であり，かつ ∑M_n が収束する場合，故に ∑u_n(x) は $\cal R$ に一様収束する．

　一様収束の重要な判定法があり，しばしば Weierstrass M test と呼ばれますが，上記に示したとおりです．

Sequences and series

A sequence, indicated by u₁, u₂, …or brief by $\langle u_n \rangle$ , is a function defined on the set of natural numbers. The sequence is said to have the limit l or to converge to l, if given any ε > 0 there exists a number N > 0 such that |u_n – l| < ε for all n > N, and in such case it is described $\lim\limits_{n \rightarrow \infty} u_n =l$ . If the sequence does not converge, it’s called that it diverges.

Consider the sequence u₁, u₁ + u₂, u₁ + u₂ + u₃, … or S₁, S₂, S₃, … where S_n = u₁ + u₂ + … + u_n. It’s called $\langle S_n \rangle$ the sequence of partial sums of the sequence $\langle u_n \rangle$ . The symbol

$\displaystyle u_1 + u_2 + u_3 + \cdots$ or $\displaystyle \sum_{n=1}^{\infty}u_n$ or briefly $\displaystyle \sum u_n$

is defined as synonymous with $\langle S_n \rangle$ and is called an infinite series. This series will converge or diverge according as $\langle S_n \rangle$ converges or diverges. If it converges to S it’s called S as the sum of the series.

The following are some important theorems concerning infinite series.

The series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converges if p > 1 and diverges if p ≤ 1.

If ∑|u_n| converges and |v_n| ≤ |u_n|, then ∑|v_n| converges.

If ∑|u_n| converges, then ∑u_n converges.

If ∑|u_n| diverges and v_n ≥ |u_n|, then ∑v_n diverges.

The series ∑|u_n|, where |u_n| = f(n) ≥ 0, converges or diverges according as $\displaystyle \int_{1}^{\infty}f(x)dx = \lim\limits_{M \rightarrow \infty}\int_{1}^{M}f(x)dx$ exists or does not exist. This theorem is often called the integral test.

The series ∑|u_n| diverges if $\displaystyle \lim\limits_{n \rightarrow \infty}|u_n| \neq 0$ . However, if $\displaystyle \lim\limits_{n \rightarrow \infty}|u_n| = 0$ the series may or may not converge.

Suppose that $\displaystyle \lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}}{n_n}\right| = r$ . Then the series ∑u_n converges (absolutely) if r < 1 and diverges if r > 1. If r = 1, no conclusion can be drawn. This theorem is often referred to as the ratio test.

数列と級数

　数列は自然数の集合に基いて定義される関数であり，次のように示されます．u₁, u₂, … 略記すると $\langle u_n \rangle$ となります．任意の ε > 0 があり，ある数 N > 0 が存在し，|u_n – l| < ε が全ての n > N について成り立つ時，この数列は極限値 l を持つ，または l に収束するといいます．そのような場合には $\lim\limits_{n \rightarrow \infty} u_n =l$ のように記述します．数列が収束しない場合は発散するといいます．

　次のような数列を考えてみます． u₁, u₁ + u₂, u₁ + u₂ + u₃, … または S₁, S₂, S₃, … ただし S_n = u₁ + u₂ + … + u_n．これを $\langle S_n \rangle$ と記述し，数列 $\langle u_n \rangle$ の部分和の数列と呼びます．その記号は

$\displaystyle u_1 + u_2 + u_3 + \cdots$ または $\displaystyle \sum_{n=1}^{\infty}u_n$ または略記して $\displaystyle \sum u_n$

のように定義し， $\langle S_n \rangle$ と同義であり無限級数と呼びます．この級数が収束するか発散するかは $\langle S_n \rangle$ が収束するか発散するかに依存します．S に収束するなら S は数列の合計と呼びます．

　以下は無限級数についてのいくつかの重要な定理です．

級数 $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ は p > 1 なら収束し， p ≤ 1 なら発散する．
∑|u_n| が収束しかつ |v_n| ≤ |u_n| なら ∑|v_n| は収束する．
∑|u_n| が収束するなら ∑u_n は収束する．
∑|u_n| が発散しかつ v_n ≥ |u_n| なら ∑v_n は発散する．
級数 ∑|u_n| ただし |u_n| = f(n) ≥ 0 が収束するか発散するかは $\displaystyle \int_{1}^{\infty}f(x)dx = \lim\limits_{M \rightarrow \infty}\int_{1}^{M}f(x)dx$ が存在するかしないかに依存する．この定理はしばしば積分判定法と呼ばれる．
級数 ∑|u_n| は $\displaystyle \lim\limits_{n \rightarrow \infty}|u_n| \neq 0$ なら発散する．しかしながら，仮に $\displaystyle \lim\limits_{n \rightarrow \infty}|u_n| = 0$ の場合，級数が収束するか発散するかは分からない．
次のように仮定してみる． $\displaystyle \lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}}{n_n}\right| = r$ . すると級数 ∑u_n converges (absolutely) は r < 1 なら収束し， r > 1 なら発散する．r = 1 の場合結論は一定ではない．この定理はしばしば比判定法として引用される．

Special types of functions

Polynomials

Polynomial is formula as below;
$\displaystyle f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \cdots + a_n$
If $a_0 \neq 0$ , n is called as degree of polynomials.
$\displaystyle (a + x)^n = a^n + \left(\frac{n}{1}\right)a^{n -1}x + \left(\frac{n}{2}\right)a^{n -2}x^2 + \cdots + x^n$
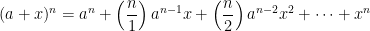
where the binomial coefficients are given by

$\displaystyle \left(\frac{n}{k}\right) = \frac{n!}{k!(n - k)!}$
and where factorial n, i.e. n! = n(n -1)(n-2)…1 while 0! = 1 by definition.

Exponential function
$\displaystyle f(x) = a^x$
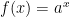
An important special case occurs where a = e = 2.718…

Exponential law

$\displaystyle a^{m + n} = a^m \cdot a^n$

$\displaystyle a^{m - n} = \frac{a^m}{a^n},\ a \neq 0$

$\displaystyle (a^m)^n = a^{mn}$

Logarithmic function
$\displaystyle f(x) = \log_a x$
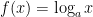
These functions are inverse of the exponential functions, i.e. if a^x = y then x = log_ay where a is called the base of the logarithm. If a = e, which is often called the natural base of logarithm, it’s described log_e by ln x, called the natural logarithm of x.

Logarithmic law

$\displaystyle \ln(mn) = \ln(m) + \ln(n)$

$\displaystyle \ln\frac{m}{n} = \ln(m) - \ln(n)$

$\displaystyle \ln{m^p} = p\ln{m}$

特殊な関数

多項式

多項式は下記のように表現します．

$\displaystyle f(x) = a_0x^n + a_1x^{n-1} + a_2x^{n-2} + \cdots + a_n$

　 $a_0 \neq 0$ の時， n は多項式の次数といいます．

$\displaystyle (a + x)^n = a^n + \left(\frac{n}{1}\right)a^{n -1}x + \left(\frac{n}{2}\right)a^{n -2}x^2 + \cdots + x^n$

二項係数は下記のように表現します．

$\displaystyle \left(\frac{n}{k}\right) = \frac{n!}{k!(n - k)!}$

n の階乗は n! = n(n -1)(n-2)…1 であり，定義上 0! = 1 となります．

指数関数

$\displaystyle f(x) = a^x$

　a = e = 2.718… の時，特殊な例が発生します．

指数法則

$\displaystyle a^{m + n} = a^m \cdot a^n$
$\displaystyle a^{m - n} = \frac{a^m}{a^n},\ a \neq 0$
$\displaystyle (a^m)^n = a^{mn}$

対数関数

$\displaystyle f(x) = \log_a x$

対数関数は指数関数の逆関数です．仮に a^x = y である時，逆関数は x = log_ay であり a は対数の底と呼びます．a = e の時，それを自然対数の底と呼び，x の自然対数 log_ex のことを ln x と表現します．

対数法則

$\displaystyle \ln(mn) = \ln(m) + \ln(n)$
$\displaystyle \ln\frac{m}{n} = \ln(m) - \ln(n)$
$\displaystyle \ln{m^p} = p\ln{m}$

Integrals

Integrals

If dy/dx = f(x), then it’s called that y an indefinite integral of f(x) and denoted as
$\displaystyle \int f(x)dx$
If $f(x) = \frac{d}{dx}F(x)$ , then
$\displaystyle \int_a^b f(x)dx = F(b) - F(a)$
Integral formulas

In the following u, v represent functions of x while a, b, c, p represent constants.
$\displaystyle \int (u \pm v)dx = \int u dx \pm \int v dx\\\vspace{0.2 in} \int cu dx = c\int u dx \\\vspace{0.2 in} \int u\left(\frac{dv}{dx}\right) = uv - \int v \left(\frac{du}{dx}\right)dx \\\vspace{0.2 in} \int u dv = uv - \int v du$
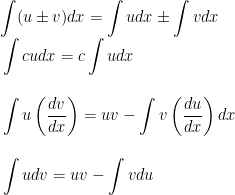
This is called integration by parts.
$\displaystyle \int F(u(x))dx = \int F(w)\frac{dw}{dw/dx}$
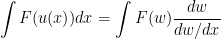
where w = u(x) and w’ = dw/dx expressed as a function of w. This is called integration by substitution or tranformation.
$\displaystyle \int u^p du = \frac{u^{p+1}}{p+1},\ p \neq -1\\\vspace{0.2 in} \int u^{-1}du = \int \frac{du}{u} = \ln u\\\vspace{0.2 in} \int a^u du = \frac{a^u}{\ln a},\ a \neq 0,\ 1\\\vspace{0.2 in} \int e^u du = e^u$
$\displaystyle \int \sin u\ du = -\cos{u}\\\vspace{0.2 in} \int \cos u\ du = \sin{u}\\\vspace{0.2 in} \int \tan u\ du = -\ln \cos{u}\\\vspace{0.2 in} \int e^{au}\sin{bu}\ du = \frac{e^{au}(a\ \sin{bu}- b\ \cos{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int e^{au}\cos{bu}\ du = \frac{e^{au}(a\ \cos{bu}+ b\ \sin{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int \frac{du}{\sqrt{a^2 - u^2}} = \sin^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{u^2 + a^2} = \frac{1}{a}\tan^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 - a^2}} = \ln(u + \sqrt{u^2 - a^2})\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 + a^2}} = \ln(u + \sqrt{u^2 + a^2})$

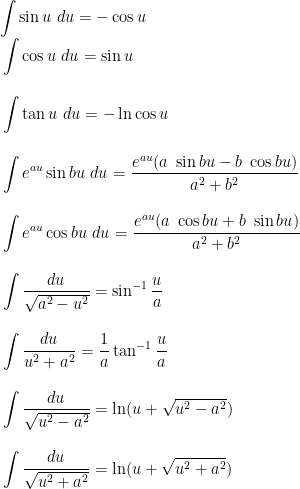
積分

　ある関数について dy/dx = f(x) である時，y は次のように表現されます．

$\displaystyle \int f(x)dx$

　 $f(x) = \frac{d}{dx}F(x)$ の時，積分は以下のように定義されます．

$\displaystyle \int_a^b f(x)dx = F(b) - F(a)$

積分公式

　関数 u, v および定数 a, b, c, p について下記が成り立ちます．

$\displaystyle \int (u \pm v)dx = \int u dx \pm \int v dx\\\vspace{0.2 in} \int cu dx = c\int u dx \\\vspace{0.2 in} \int u\left(\frac{dv}{dx}\right) = uv - \int v \left(\frac{du}{dx}\right)dx \\\vspace{0.2 in} \int u dv = uv - \int v du \\\vspace{0.2 in} \int F(u(x))dx = \int F(w)\frac{dw}{dw/dx},\ w = u(x)$ $\displaystyle \int u^p du = \frac{u^{p+1}}{p+1},\ p \neq -1\\\vspace{0.2 in} \int u^{-1}du = \int \frac{du}{u} = \ln u\\\vspace{0.2 in} \int a^u du = \frac{a^u}{\ln a},\ a \neq 0,\ 1\\\vspace{0.2 in} \int e^u du = e^u$ $\displaystyle \int \sin u\ du = -\cos{u}\\\vspace{0.2 in} \int \cos u\ du = \sin{u}\\\vspace{0.2 in} \int \tan u\ du = -\ln \cos{u}\\\vspace{0.2 in} \int e^{au}\sin{bu}\ du = \frac{e^{au}(a\ \sin{bu}- b\ \cos{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int e^{au}\cos{bu}\ du = \frac{e^{au}(a\ \cos{bu}+ b\ \sin{bu})}{a^2 + b^2}\\\vspace{0.2 in} \int \frac{du}{\sqrt{a^2 - u^2}} = \sin^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{u^2 + a^2} = \frac{1}{a}\tan^{-1}\frac{u}{a}\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 - a^2}} = \ln(u + \sqrt{u^2 - a^2})\\\vspace{0.2 in} \int \frac{du}{\sqrt{u^2 + a^2}} = \ln(u + \sqrt{u^2 + a^2})$

月	火	水	木	金	土	日
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31