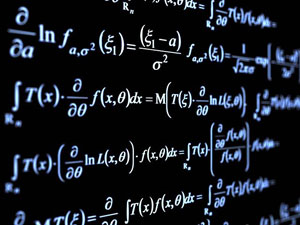日: 2014年7月14日

DOUBLE INTEGRALS

Fig. 6-1

Let F(x, y) be defined in a closed region \cal R of the xy plane. Subdivided \cal R into n subregions \Delta\cal R of area \Delta A_k,\ k = 1,\ 2,\ \dots,\ n. Let (\xi_k, \eta_k) be some point of \Delta\cal R. Form the sum

\displaystyle \sum_{k=1}^{n}F(\xi_k, \eta_k)\Delta A_k\cdots(1)

Consider

\displaystyle \lim\limits_{n\rightarrow\infty}\sum^{n}_{k=1}F(\xi_k, \eta_k)\Delta A_k\cdots(2)

where the limit is taken so that the number n of subdivisions increases without limit and such that the largest linear dimension of each \Delta \cal R approaches zero. If this limit exists it is denoted by

\displaystyle \iint_{\cal R}F(x, y)dA\cdots(3)

and is called the double integral of F(x, y) over the region \cal R.

It can be proved that the limit dose exist if F(x, y) is continuous (or piecewise continuous) in \cal R.

二重積分

Fig. 6-1

F(x, y) を xy 平面の閉領域 \cal R 内に定義します． \cal R を面積が \Delta A_k,\ k = 1,\ 2,\ \dots,\ n で n 個の小領域 \Delta\cal R に細分化します． (\xi_k, \eta_k) を \Delta\cal R のある点とします．次のように和を形成します．

\displaystyle \sum_{k=1}^{n}F(\xi_k, \eta_k)\Delta A_k\cdots(1)

以下を考えてみましょう．

\displaystyle \lim\limits_{n\rightarrow\infty}\sum^{n}_{k=1}F(\xi_k, \eta_k)\Delta A_k\cdots(2)

ここで極限は細分化された n の数が無限に増大し，またそれぞれの \Delta \cal R の最大長の次元はゼロに近づいていくものとします．このような極限が存在する時，次のように記述します．

\displaystyle \iint_{\cal R}F(x, y)dA\cdots(3)

そしてこれを領域 \cal R における F(x, y) の 二重積分 と呼びます．

仮に \cal R において F(x, y) が連続，または区間的に連続なら極限は存在すると証明できます．