Theorems on eigenvalues and eigenvectors

Theorem 12. The eigenvalues of a Hermitian matrix [or symmetric real matrix] are real. The eigenvalues of a skew-Hermitian matrix [or skew-symmetric real matrix] are zero or pure imaginary. The eigenvalues of a unitary [or real orthogonal matrix] all have absolute value equal to 1.

Theorem 13. The eigenvectors belonging to different eigenvalues of a Hermitian matrix [or symmetric real matrix] are orthogonal.

Theorem 14. [Cayley-Hamilton] A matrix satisfies its own characteristic equation.

Theorem 15. [reduction of matrix to diagonal form] If a non-singular matrix $A$ has distinct eigenvalues $\lambda_1,\ \lambda_2,\ \cdots$ with corresponding eigenvectors written as columns in the matrix

$\displaystyle B = \left( \begin{array}{cccc} b_{11} & b_{12} & b_{13} & \cdots \\ b_{21} & b_{22} & b_{23} & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array} \right)$

then

$B^{-1}AB = \left( \begin{array}{cccc} \lambda_1 & 0 & 0 & \cdots \\ 0 & \lambda_2 & 0 & \cdots \\ 0 & 0 & \lambda_3 & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array} \right)$

i.e. $B^{-1}AB$ , called the transform of $A$ by $B$ , is a diagonal matrix containing the eigenvalues of $A$ in the main diagonal and zeros elsewhere. We say that $A$ has been transformed or reduced to diagonal form.

Theorem 16. [Reduction of quadratic form to canonical form] Let $A$ be a symmetric matrix, for example,

$\displaystyle A = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right),\ a_{12} = a_{21},\ a_{13} = a_{11},\ a_{23} = a_{32}$

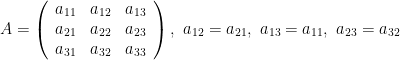
Then if $\displaystyle X = \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right)$ , we obtain the quadratic form

$X^TAX = a_{11}x_1^2 + a_{22}x_2^2 + a_{33}x_3^2 + 2a_{12}x_1x_2 + 2a_{13}x_1x_3 + 2a_{23}x_2x_3$

The cross product terms of this quadratic form can be removed by letting $X = BU$ where $U$ is the column vector with elements $u_1,\ u_2,\ u_3$ and $B$ is an orthogonal matrix which diagonalizes $A$ . The new quadratic form in $u_1,\ u_2,\ u_3$ with no cross product terms is called the canonical form. A generalization can be made to Hermitian quadratic forms.