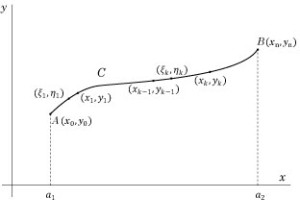
 Fig. 6-2
Fig. 6-2
仮に平面  における曲線 C の式が
における曲線 C の式が 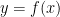 で与えられるなら,積分の定義を得るために線積分 (14) は被積分関数内で
で与えられるなら,積分の定義を得るために線積分 (14) は被積分関数内で 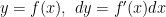 と置換されて評価されます.
と置換されて評価されます.
![\displaystyle \int_{a_1}^{a_2}[P\{x, f(x)\}dx + Q\{x, f(x)\}f'(x)dx] \cdots(19) \displaystyle \int_{a_1}^{a_2}[P\{x, f(x)\}dx + Q\{x, f(x)\}f'(x)dx] \cdots(19)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7Ba_1%7D%5E%7Ba_2%7D%5BP%5C%7Bx%2C+f%28x%29%5C%7Ddx+%2B+Q%5C%7Bx%2C+f%28x%29%5C%7Df%27%28x%29dx%5D+%5Ccdots%2819%29&bg=T&fg=000000&s=0)
上記は通常の方法で評価します.
同様に仮に C が 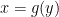 として与えられるなら
として与えられるなら 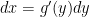 となり線積分は以下のようになります.
となり線積分は以下のようになります.
![\displaystyle \int_{b_1}^{b_2}[P\{g(y), y\}g'(y)dy + Q\{g(y), y\}dy]\cdots(20) \displaystyle \int_{b_1}^{b_2}[P\{g(y), y\}g'(y)dy + Q\{g(y), y\}dy]\cdots(20)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7Bb_1%7D%5E%7Bb_2%7D%5BP%5C%7Bg%28y%29%2C+y%5C%7Dg%27%28y%29dy+%2B+Q%5C%7Bg%28y%29%2C+y%5C%7Ddy%5D%5Ccdots%2820%29&bg=T&fg=000000&s=0)
仮に C がパラメーター形式  で与えられるなら,線積分は以下のようになります.
で与えられるなら,線積分は以下のようになります.
![\displaystyle \int_{t_1}^{t_2} [P\{ \phi(t),\ \psi(t) \}\phi'(t)dt + Q\{ \phi(t),\ \psi(t) \}\psi'(t)dt] \cdots (21) \displaystyle \int_{t_1}^{t_2} [P\{ \phi(t),\ \psi(t) \}\phi'(t)dt + Q\{ \phi(t),\ \psi(t) \}\psi'(t)dt] \cdots (21)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7Bt_1%7D%5E%7Bt_2%7D+%5BP%5C%7B+%5Cphi%28t%29%2C%5C+%5Cpsi%28t%29+%5C%7D%5Cphi%27%28t%29dt+%2B+Q%5C%7B+%5Cphi%28t%29%2C%5C+%5Cpsi%28t%29+%5C%7D%5Cpsi%27%28t%29dt%5D+%5Ccdots+%2821%29&bg=T&fg=000000&s=0)
ここで 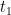 および
および 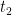 は点
は点 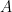 および点
および点 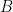 に対応する
に対応する 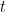 の値を示します.
の値を示します.
上記方法の組み合わせを評価に用います.
同様の方法で空間曲線に沿った線積分の評価を行います.