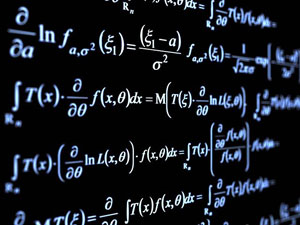Systems of n equations in n unknowns. Cramer’s rule

If $m = n$ and if $A$ is a non-singular matrix so that $A^{-1}$ exists, we can solve (17) or (18) by writing
$X = A^{-1}R \cdots(19)$
and the system has a unique solution.

Alternatively we can express the unknowns $x_1,\ x_2,\ \cdots,\ x_n$ as
$\displaystyle x_1 = \frac{\Delta_1}{\Delta},\ x_2 = \frac{\Delta_2}{\Delta},\ \cdots,\ x_n = \frac{\Delta_n}{\Delta} \cdots (20)$
where $\Delta = \det(A)$ , called the determinant of the system, is given by (9) and $\Delta_k,\ k = 1,\ 2,\ \cdots,\ n$ is the determinant obtained from $\Delta$ by removing the kth column and replacing it by the column vector $R$ . The rule expressed in (20) is called Cramer’s rule.

The following four cases can arise.

Case 1, $\Delta \ne 0,\ R \ne 0$ . In this case there will be a unique solution where not all $x_k$ will be zero.

Case 2, $\Delta \ne 0,\ R = 0$ . In this case the only solution will be $x_1 = 0,\ x_2 = 0,\ \cdots,\ x_n = 0$ , i.e. $X = 0$ . This is often called the trivial solution.

Case 3, $\Delta = 0,\ R = 0$ . In this case there will be infinitely many solutions other than the trivial solution. This means that at least one of the equations can be obtained from the others, i.e. the equations are linearly dependent.

Case 4, $\Delta = 0,\ R \ne 0$ . In this case infinitely many solutions will exist if and only if all of the determinants $\Delta_k$ in (20) are zero. Otherwise there will be no solution.